Giúp mình gấp với ạ
Cho hình chóp S.ABCD có đáy là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Gọi (α) là mặt phẳng đi qua O và song song với AB, SC. Xác định thiết diện tạo bởi (α) và hình chóp? Thiết diện là hình gì?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

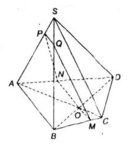
+ Ta có: (α) // AB
⇒ giao tuyến (α) và (ABCD) là đường thẳng qua O và song song với AB.
Qua O kẻ MN // AB (M ∈ BC, N ∈ AD)
⇒ (α) ∩ (ABCD) = MN.
+ (α) // SC
⇒ giao tuyến của (α) và (SBC) là đường thẳng qua M và song song với SC.
Kẻ MQ // SC (Q ∈ SB).
+ (α) // AB
⇒ giao tuyến của (α) và (SAB) là đường thẳng qua Q và song song với AB.
Từ Q kẻ QP // AB (P ∈ SA).
⇒ (α) ∩ (SAD) = PN.
Vậy thiết diện của hình chóp cắt bởi (α) là tứ giác MNPQ.
Ta có: PQ// AB và NM // AB
=> PQ // NM
Do đó, tứ giác MNPQ là hình thang.

Đáp án D
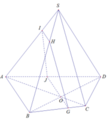
Trong mặt phẳng (ABCD), kẻ đường thẳng d đi qua O và song song với AB
d cắt AD tại J
d cắt BC tại G
Trong mặt phẳng (SBC), kẻ đường thẳng Gx đi qua G và song song với SC; đường thẳng này cắt SB tại H
Trong mặt phẳng (SAB), kẻ đường thẳng y đi qua H và song song với AB
y cắt SA tại I
⇒ IHGJ là thiết diện cần tìm
Xét tứ giác IHGJ có: IH // JG ( // AB )
⇒ IHGJ là hình thang

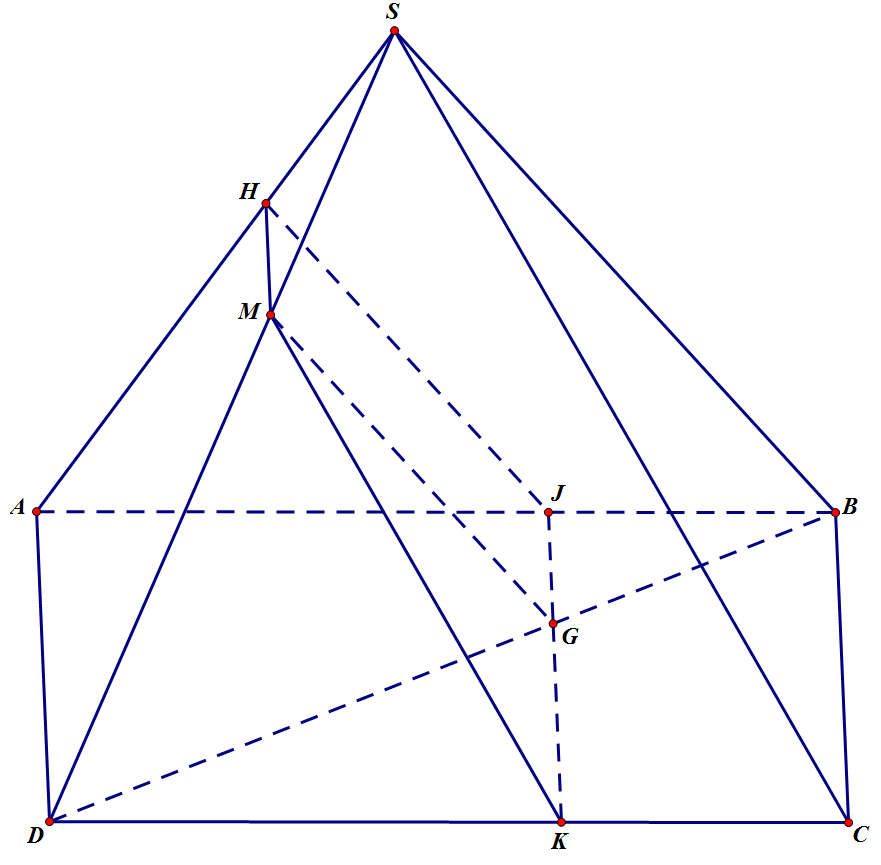
(α) và (SAD) cùng chứa điểm M. Mà (α) // AD nên (α) \(\cap\) (SAD) = d1 với d1 là đường thẳng đi qua M và song song với AD.
Trong (SAD) gọi H = d1 \(\cap\) SA ⇒ (SAD) \(\cap\) (α) = MH
(α) và (SBD) cùng chứa điểm M. Mà (α) // SB nên (α) \(\cap\) (SBD) = d2 với d2 là đường thẳng đi qua M và song song với SB.
Trong (SBD) gọi G = d2 \(\cap\) BD ⇒ (SAD) \(\cap\) (α) = MG
(SAB) và (α) cùng chứa điểm H. Mà (SAB) chứa SB, (α) chứa MG và ta lại có MG // SB
⇒ (SAB) \(\cap\) (α) = d3 với d3 là đường thẳng đi qua H và song song với SB và MG
Trong (SAB) gọi J = \(d_3\cap AB\) ⇒ (SAB) \(\cap\) (α) = HJ
Trong (ABCD) gọi K = JG \(\cap\) CD
Thiết diện cần tìm là tứ giác HMKJ (hình thang hai đáy HM, JK)
*Lưu ý : (α) không cắt (SBC) vì (α) // (SBC).
\(\cap\)

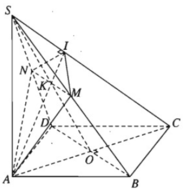
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
b) Ta có 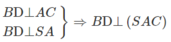
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.
a, Giả thiết cho biết (α) và(ABCD) cùng chứa điểm O
Mà (α) // AB ⇒ (α) chứa đường thẳng song song với AB
⇒ (α) \(\cap\) (ABCD) = d1 . Với d1 là đường thẳng đi qua O và song song với AB. Trong (ABCD) gọi \(\left\{{}\begin{matrix}G=d_1\cap AD\\H=d_1\cap BC\end{matrix}\right.\)
⇒ (α) \(\cap\) (ABCD) = GH (hình vẽ)
Giả thiết cho biết :
Giả thiết cho biết (α) và (SAC) cùng chứa điểm O
Mà (α) // SC ⇒ (α) chứa đường thẳng song song với SC
⇒ (α) \(\cap\) (SAC) = d2 . Với d2 là đường thẳng đi qua O và song song với SC. Trong (SAC) gọi I = d2 \(\cap\) SA
⇒ (α) \(\cap\) (SAC) = O\(I\) (hình vẽ)
(P) và (SAB) cùng chứa điểm I. Mà (P) chứa GH, (SAB) chứa AB. Mà ta lại có AB // GH
⇒ (P) \(\cap\) (SAB) = d3. Với d3 là đường thẳng đi qua I và song song với AB và GH
Trong (SAB), gọi J = \(d_3\cap SB\)
⇒ Thiết diện cần tìm là tứ giác IJHG
Tứ giác này có IJ // HG nên nó là hình thang