Tính diện tích tam giác biết độ dài 3 đường cao là 3cm,4cm và 2,4cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
Áp dụng HTL: \(AH\cdot BC=AB\cdot AC\Leftrightarrow AH=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\)
Vì M là trung điểm BC nên chia tam giác ABC ra 2 tam giác ABM và ACM có diện tích bằng nhau và cùng bằng một nửa diện tích ABC
Mà \(S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
Vậy \(S_{ABM}=\dfrac{1}{2}S_{ABC}=3\left(cm^2\right)\)

Diện tích hình tam giác đó là :
4 x 3 : 2 = 6 ( cm2 )
Đáp số : 6 cm2
^ - ^

Độ dài cạnh đáy là:
$10,2\times2:4=5,1(cm)$
Vì không có đáp án nào đúng nên ta không chọn đáp án nào cả.
Stam giác = \(\dfrac{1}{2}\) ✖ đường cao ✖ cạnh đáy
⇒ Độ dài cạnh đáy = \(\dfrac{2\cdot10,2}{4}=5,1\left(cm\right)\)

a) Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{HAB}\right)\)
Do đó: ΔHBA\(\sim\)ΔHAC(g-g)

diện tích tam giác là 3*4/2=6cm2
đáy là 6*2/2,4=5cm
suy ra đường kính tròn là 5cm
bán kính là 5/2=2,5cm
diện tích là 2,582,583,14=19,625 cm2
đ/s:19,625cm2

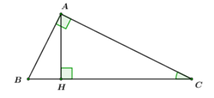
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
![]()
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
![]()
![]()
Đáp án cần chọn là: B