Cho 0o <góc anpha <45 .
Chứng minh :sin 2 anpha = 2 sin anpha x cos .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
1
VT
13 tháng 11 2019
Công thức của định luật khúc xạ: n1 sini=n2 sinr
Trường hợp i=0o= >r=0
Kết luận: Tia sáng qua mặt phân cách của hai môi trường có phương theo phương vuông góc với mặt phân cách không bị khúc xạ.
10 tháng 9 2023
a: Ta sẽ có hình vẽ sau:
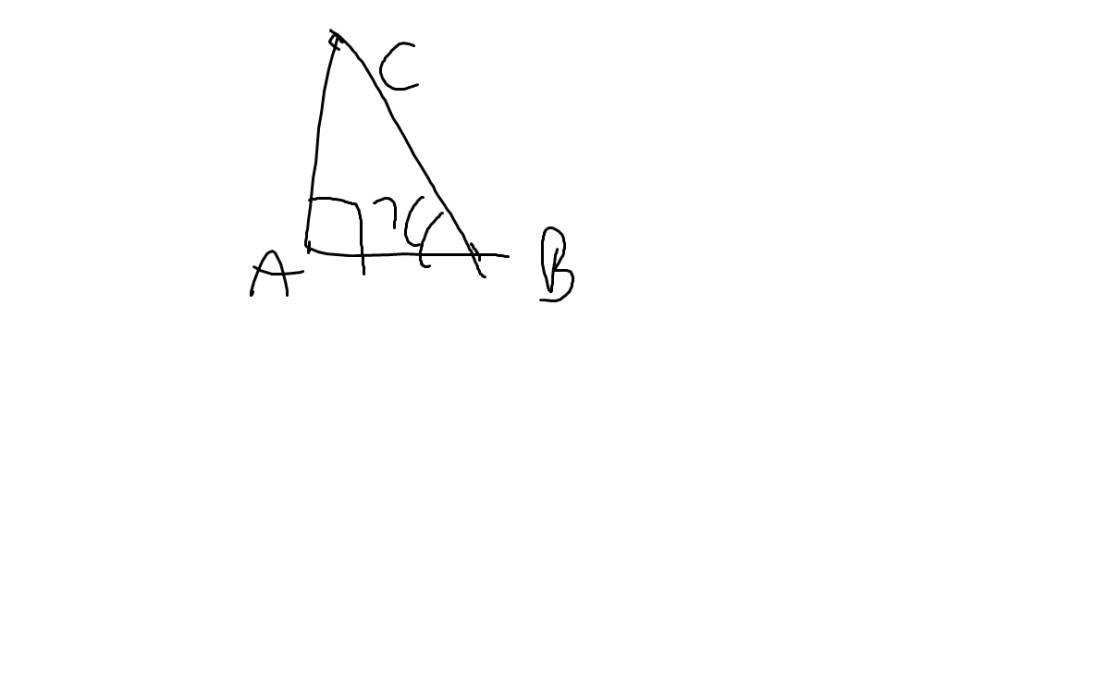
Đặt \(x=\widehat{B}\)
sin x=sin B=AC/BC
cosx=cosB=AB/BC
\(tanx=tanB=\dfrac{AC}{AB}=\dfrac{sinx}{cosx}\)
=>\(tan^2x=\dfrac{sin^2x}{cos^2x}\)
b: \(cot^2x=\dfrac{1}{tan^2x}=1:\dfrac{sin^2x}{cos^2x}=\dfrac{cos^2x}{sin^2x}\)
1 tháng 8 2016
100g=0,1kg
a)ta có phương trình cân bằng nhiệt:
Qtỏa=Qthu
\(\Leftrightarrow Q=m_1C_1\left(t-t_1\right)\)
\(\Leftrightarrow Q=180\left(0--7,5\right)=1350J\)
b)gọi m là số nước đá tan
150g=0,15kg
ta có phương trình cân bằng nhiệt:
Qtỏa=Qthu
\(Q_2=Q_1\)
\(\Leftrightarrow m_2C_2\left(t_2-t\right)=m\lambda\)
\(\Leftrightarrow57\left(100-0\right)=3,4.10^5m\)
\(\Leftrightarrow5700=3,4.10^5m\Rightarrow m=0,016kg\)
TN
với 0o < a < 90o cho sin a = 3 cos a khi đó tính 4 - sina cosa tâ được kết quả là:
A.3
B.3,5
C.3,7
D.3,9
1
N
19 tháng 11 2021
\(\sin^2\alpha+\cos^2\alpha=1\Leftrightarrow10\cos^2\alpha=1\Leftrightarrow\cos\alpha=\sqrt{\dfrac{1}{10}}=\dfrac{\sqrt{10}}{10}\\ \Leftrightarrow\sin\alpha=\dfrac{3\sqrt{10}}{10}\\ \Leftrightarrow4-\sin\alpha\cdot\cos\alpha=4-\dfrac{\sqrt{10}\cdot3\sqrt{10}}{100}=4-\dfrac{3}{10}=3,7\)
Vậy chọn C
8 tháng 8 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
=>DE/BC=AD/AB=cosA
=>DE=BC*cosA
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp đường tròn đường kính BC
=>M là tâm đường tròn ngoại tiếp tứ giác BEDC
ΔMDE đều khi MD=ME=DE
=>MD=BC*cosA
mà MD=BC/2
nên BC/2=BC*cosA
=>BC*cosA-BC/2=0
=>\(BC\cdot\left(cosA-\dfrac{1}{2}\right)=0\)
=>\(cosA=\dfrac{1}{2}\)
=>\(\widehat{A}=60^0\)
CM
13 tháng 4 2019
Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.
CM
20 tháng 8 2019
Xét hàm số
V T = 999 , 87 - 0 , 06426 T + 0 , 0085043 T 2 - 0 , 0000679 T 3
với T ∈ 0 ; 30
V ' T = - 0 , 06426 + 0 , 0170086 T - 2 , 037 . 10 - 4 T 2
V ' T = 0 ⇔ T ≈ 2 , 9665 T ≈ 79 , 5317 . Do T ∈ 0 ; 30 nên loại nghiệm T ≈ 79 , 5317 o C
Lập bảng biến thiên và suy ra V đạt giá trị nhỏ nhất tại T ≈ 3 , 9665 o C
Đáp án A