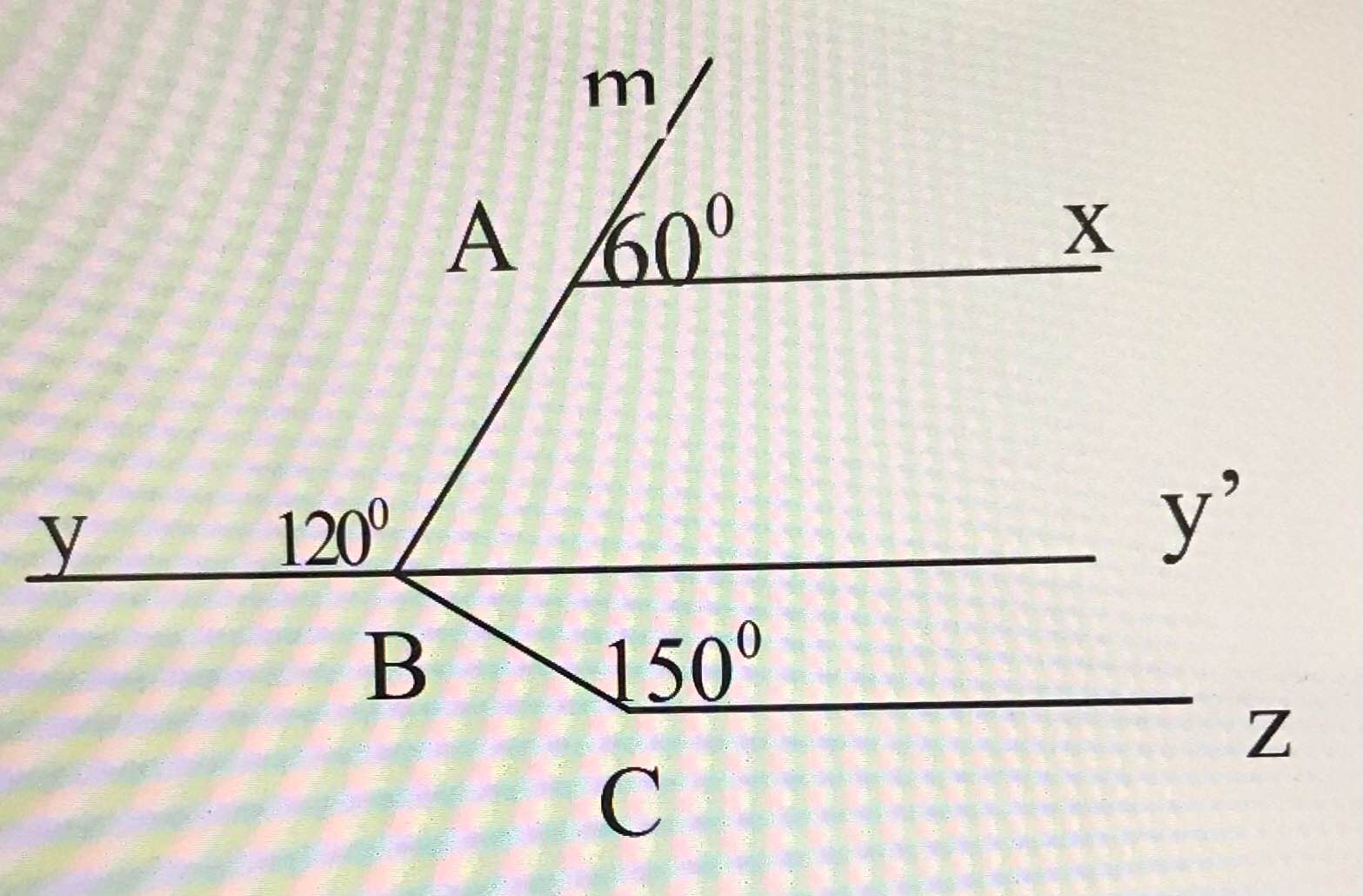
Trong hình vẽ bên, cho ABC ̂ = 800, By là tia phân giác của ABC ̂.Chứng minh rằng:a) Ax ⫽ By theo hai cách b) Ax ⫽...
Đọc tiếp
Trong hình vẽ bên, cho ABC ̂ = 800, By là tia phân giác của ABC ̂.
Chứng minh rằng:
a) Ax ⫽ By theo hai cách b) Ax ⫽ Cz
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
15 tháng 6 2018
a) Ta có tAx ^ + xAB ^ = 180 ∘ (hai góc kề bù) mà tAx ^ = 60 ∘
⇒ xAB ^ = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác ABy ^ = 120 ∘
⇒ xAB ^ = ABy ^ mà hai góc này ở vị trí so le trong
⇒ Ax // By
b)
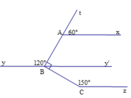
Kẻ tia By' là tia đối của tia By
Ta có: ABy ^ + ABy' ^ = 180 ∘ (hai góc kề bù) mà ABy ^ = 120 ∘
⇒ ABy' ^ = 180 ∘ − 120 ∘ = 60 ∘
Mặt khác ABC ^ = 90 ∘ hay ABy' ^ + y'BC ^ = 90 ∘
⇒ y'BC ^ = 90 ∘ − 60 ∘ = 30 ∘
Ta có y'BC ^ + CBy ^ = 180 ∘ (hai góc kề bù)
⇒ CBy ^ = 180 ∘ − 30 ∘ = 150 ∘
Ta lại có BCz ^ = 150 ∘
⇒ BCz ^ = CBy ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
CM
9 tháng 3 2018
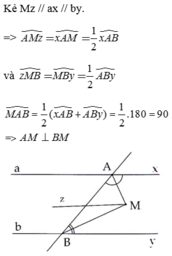
Kẻ M z / / a x / / b y
Vì AM là tia phân giác của x A B ^
⇒ A M z ^ = x A M ^ = 1 2 x A B ^
BM là phân giác của A B y ^
⇒ A B M ^ = M B y ^ = 1 2 A B y ^
Ta có: M z / / a x nên A M z ^ = M A x ^ (hai góc so le trong)
M z / / b y nên z M B ^ = B M y ^ (hai góc so le trong)
⇒ A M B ^ = A M z ^ + z M B ^ = 1 2 x A B ^ + A B y ^ = 1 2 ⋅ 180 0 = 90 0
Vậy A M ⊥ B M (đpcm)
NQ
0
CM
20 tháng 6 2019
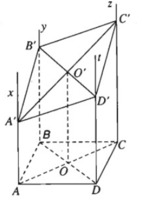
a) Ta có:
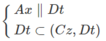
⇒ Ax // (Cz,Dt)
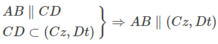
Từ Ax, AB ⊂ (Ax,By) suy ra (Ax, By) // (Cz, Dt)
Tương tự ta có (Ax, Dt) // (By,Cz)
b)
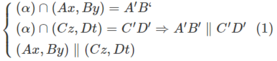
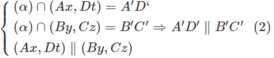
Từ (1) và (2) suy ra tứ giác A’B’C’D’ là hình bình hành.
c) Gọi O, O’ lần lượt là tâm các hình bình hành ABCD, A’B’C’D’. Dễ thấy OO’ là đường trung bình của hình thang AA’, suy ra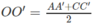 
Tương tự ta có:
VD
2
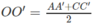
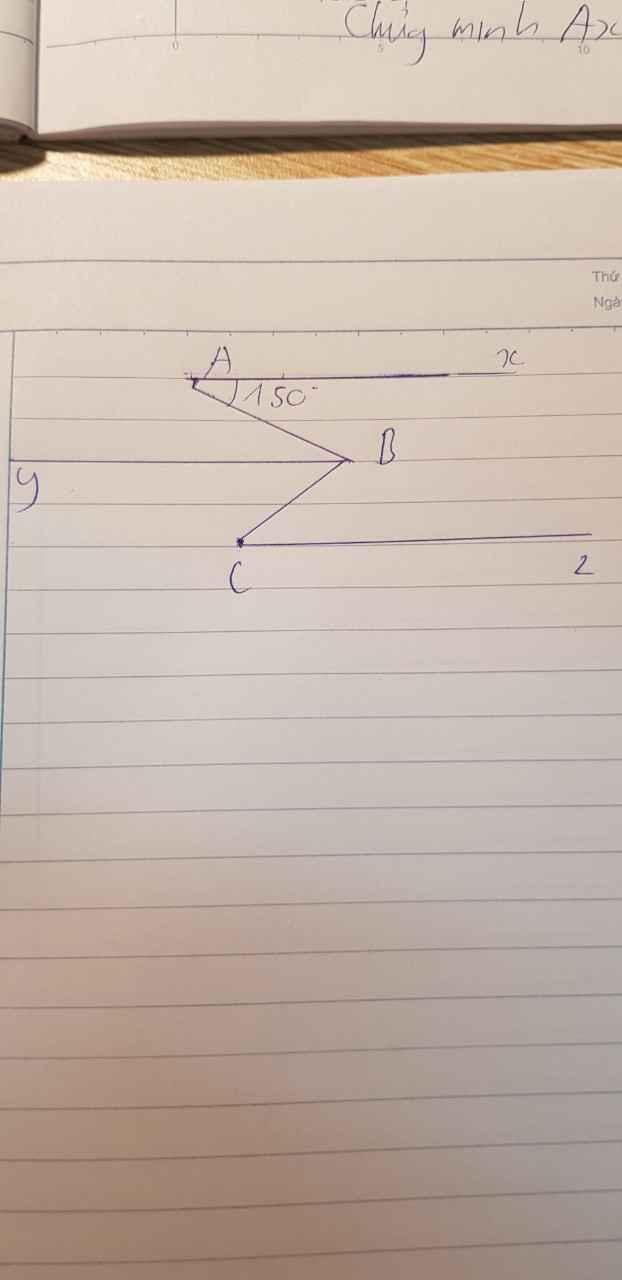
ABC=80* đấy