2 vật cách nhsu 8 cm thì Fhd =125.25*10^-9 N .Tính kl mỗi vật trong 3 trường hợp :
a, hai vật có kl bằng nhau
b,m1 =3m2
c,tổng khối lượng 2 vật bằng 8 kg
Giup mk bài này vs cho mk xin lời giải chi tiết nhé...cảm ơn nhìu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
2
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
24 tháng 7 2015
Bài này còn có một cách suy luận nhanh là thế này: Ta biết dao động điều hòa là hình chiếu của 1 chuyển động tròn lên một trục tọa độ, mà vận tốc cực đại của dao động chính là tốc độ của chuyển động tròn đều.
Khi qua VTCB, vật m1, m2 cùng đạt tốc độ cực đại, trong khi m1 tiếp tục dao động điều hòa thì m2 lại chuyển động thẳng đều.
Như vậy, trong thời gian m1 đi từ VTCB ra biên thì m2 chuyển động trên cung tròn tương ứng ( bằng 1/4 vòng tròn).
+ Ta có biên độ dao động của m1 là 4cm.
+ Quãng đường m2 chuyển động là 1/4 chu vi của đường tròn tương ứng là: 1/4. 2π.R=1/4. 2π.4=2π cm
Từ đó suy ra khoảng cách 2 vật.
17 tháng 1 2022
a) Khối lượng của 2 vật khi 2 vật có khối lượng bằng nhau :
\(F_{hd}=G\dfrac{m_1m_2}{r^2}\Rightarrow F_{hd}=G\dfrac{m^2}{r^2}\Rightarrow m^2=\dfrac{F_{hd}.r^2}{G}\)
\(\Rightarrow m=\sqrt{\dfrac{F_{hd}.r^2}{G}}=\sqrt{\dfrac{125,25.10^{-9}.\left(0,08\right)^2}{6,67.10^{-11}}}=3,4669742\left(kg\right)\)
VT
27 tháng 8 2017
Đáp án D
Ta có thể chia quá trình diễn ra của bài toán thành hai giai đoạn sau:
Giai đoạn 1: Hệ con lắc gồm lò xo có độ cứng k và vật m = m 1 + m 2 dao động điều hòa với biên độ A = 8 cm quanh vị trí cân bằng O (vị trí lò xo không biến dạng.
+ Tần số góc của dao động:
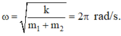
+ Tốc độ của hệ hai vật khi đi qua vị trí cân bằng v 0 = ωA = 16 π cm/s.
Giai đoạn 2: Vật m 2 tách ra khỏi vật m 1 tại O chuyển động thẳng đều với vận tốc v 0 , vật m 1 vẫn dao động điều hòa quanh O.
+ Tần số góc của dao động m 1 :
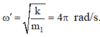
+ Biên độ dao động của m 1 :
Lò xo giãn cực đại lần đầu tiên ứng với m 1 đang ở vị trí biên, khi đó m 2 đã chuyển động với khoảng thời gian tương ứng là ∆ t = T ' 4 = 1 8 s.
Khoảng cách giữa hai vật:
VT
25 tháng 1 2017
Đáp án A
+ Ban đầu hệ nằm yên khi đó lò xo dán một đoạn Δ l = q E k = 1 c m
+ Sau khi cắt dây nối vật A, B thì
Vật A dao động điều hòa với biên độ
+ Khi lò xo có chiều dài ngắn nhất lần đầu tiên:
· Vật A đang ở biên âm → lò xo đang bị nén đoạn 1cm → Vật A cách vị trí ban đầu một đoạn X = 2A = 2 cm
Vật B chuyển động được quãng đường
VT
24 tháng 5 2019
Vật B chuyển động cùng chiều với điện trường dưới tác dụng của lực điện gây ra gia tốc
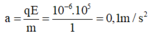
+ Chiều dài lò xo ngắn nhất lần đầu tiên ứng với khoảng thời gian 0,5T kể từ khi dây nối bị đứt, vật A đến vị trí lò xo bị nén 1cm
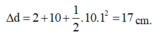
Đáp án A
VT
8 tháng 10 2019
Đáp án A
Ban đầu hệ nằm yên khi đó lò xo dán một đoạn Δ l = q E k = 1 c m
Sau khi cắt dây nối vật A, B thì
- Vật A dao động điều hòa với biên độ A = Δ l = 1 c m ; T = 2 π m k = 2 s
- Vật B chuyển động nhanh dần đều với gia tốc a = q E m = 0 , 1 m / s 2
Khi lò xo có chiều dài ngắn nhất lần đầu tiên:
- Vật A đang ở biên âm → lò xo đang bị nén đoạn 1cm → Vật A cách vị trí ban đầu một đoạn X = 2 A = 2 c m
- Vật B chuyển động được quãng đường S = 1 2 a t 2 = 1 2 a T 2 2 = 1 2 .0 , 1.1 2 = 0 , 05 m = 5 c m
Vậy khoảng cách giữa hai vật A, B lúc này: d = X + l + S = 2 + 10 + 5 = 17 c m
OT
22 tháng 2 2018
a) ta có : hai vật có khối lượng bằng nhau
\(\Rightarrow F_{hd}=G\dfrac{m_1m_2}{r^2}=6,67.10^{-11}.\dfrac{m_1^2}{\left(0,08\right)^2}=125,25.10^{-9}\)
\(\Leftrightarrow m_1^2=\dfrac{125,25.10^{-9}.\left(0,08\right)^2}{6,67.10^{-11}}=\dfrac{8016}{667}\) \(\Rightarrow m_1=\sqrt{\dfrac{8016}{667}}\simeq3,5\)
\(\Rightarrow m_1=m_2\simeq3,5\)
vậy khối lượng của 2 vật là \(m_1=m_2=3,5\)
b) đặc \(x\) là khối lượng của vật nhỏ \(\Rightarrow3x\) là khối lượng của vật to
vì khối lượng tổng cộng của 2 vật là \(8\) \(\Rightarrow x+3x=8\Leftrightarrow4x=8\Leftrightarrow x=\dfrac{8}{4}=2\)
vậy khối lượng của vật nhỏ là \(2\) và khối lượng của vật to là \(3.2=6\)
thế vào công thức ta có : \(\Rightarrow F_{hd}=G\dfrac{m_1m_2}{r^2}=6,67.10^{-11}.\dfrac{2.6}{\left(0,08\right)^2}=125,25.10^{-9}\) (sai)
vậy không có khối lượng của 2 vật cần tìm
Áp dụng công thức tính lực hấp dẫn: \(F=G.\dfrac{m_1m_2}{r^2}\)
Thay \(F=125,25.10^{-9}\); \(G=6,67.10^{-11}\) ; \(r=8cm=0,08m\)
Vào phương trình trên ta được:
\(125,25.10^{-9}=6,67.10^{-11}.\dfrac{m_1m_2}{(0,08)^2}\)
\(\Rightarrow m_1.m_2\approx 12\) (*)
a) Hai vật có khối lượng bằng nhau
Suy ra \(m_1=m_2=\sqrt{12}=2\sqrt 3(kg)\)
b) \(m_1=3m_2\)
Thay vào phương trình (*) ta được: \(3m_2^2=12\Rightarrow m_2=2(kg)\)
\(m_1=3m_2=3.2=6(kg)\)
c) Tổng khối lượng hai vật: \(m_1+m_2=8\)
Suy ra: \(m_2=8-m_1\)
Thay vào (*) ta được: \(m_1.(8-m_1)=12\)
\(\Rightarrow m_1^2-8m_1+12=0\)
\(\Rightarrow m_1=2(kg)\) hoặc \(m_1=6(kg)\)
Tương ứng với \(m_2=6 (kg)\) hoặc \(m_2=2(kg)\)
a, Có 8cm=0,08m
Fhd=G.\(\dfrac{m1.m2}{0,08^2}\)=6,68.10-11.\(\dfrac{2m}{0,08^2}\)=125,25.10-9
=>m=m1=m2=6kg
b, Fhd=G.\(\dfrac{m1.m2}{0,08^2}\)=6,68.10-11.\(\dfrac{3.m1^2}{0,08^2}\)=125,25.10-9
=>m1=2kg=>m2=6kg
c, m1+m2=8=>m2=8-m1
Fhd=G.\(\dfrac{m1.m2}{0,08^2}\)=6,68.10-11.\(\dfrac{m1.(8-m1)}{0,08^2}\)=125,25.10-9
=>m1=2kg=>m2=6kg