Cho am giác ABC vuông tại A.Gọi M,N,P lần lượt là trung điểm của AB,AC,BC.Gọi D,E lần lượt là điểm đối xứng của P qua M và N.a)Tính AP và diện tích tam giác ABC biết rầng AB=6cm và AC=8cmb)Chứng minh tứ giác AMPN là hình chữ nhậtc)Chứng minh tứ giác APCE là hình thoid)Tam giác ABC cần có thêm điều kiện gì để tứ giác APCE là hình vuông e)Chứng minh AP,BE,CD đồng...
Đọc tiếp
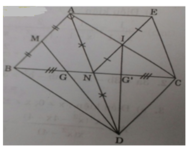
Cho am giác ABC vuông tại A.Gọi M,N,P lần lượt là trung điểm của AB,AC,BC.Gọi D,E lần lượt là điểm đối xứng của P qua M và N.
a)Tính AP và diện tích tam giác ABC biết rầng AB=6cm và AC=8cm
b)Chứng minh tứ giác AMPN là hình chữ nhật
c)Chứng minh tứ giác APCE là hình thoi
d)Tam giác ABC cần có thêm điều kiện gì để tứ giác APCE là hình vuông e)Chứng minh AP,BE,CD đồng quy
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Ta có: ΔABC vuông tại A
mà AP là đường trung tuyến ứng với cạnh huyền BC
nên \(AP=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
b: Xét ΔABC có
P là trung điểm của BC
N là trung điểm của AC
Do đó: PN là đường trung bình của ΔABC
Suy ra: PN//AB và \(PN=\dfrac{AB}{2}\)
mà \(AM=\dfrac{AB}{2}\)
nên PN//AM và PN=AM
Xét tứ giác AMPN có
PN//AM
PN=AM
Do đó: AMPN là hình bình hành
mà \(\widehat{NAM}=90^0\)
nên AMPN là hình chữ nhật
c: Xét tứ giác APCE có
N là trung điểm của đường chéo AC
N là trung điểm của đường chéo PE
Do đó: APCE là hình bình hành
mà PE\(\perp\)AC
nên APCE là hình thoi