Sin13x + sin14x = 1. Cos6x - sin6x = 13/8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
NN
2
6 tháng 9 2021
\(y=\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\)
\(\sin^6x+\cos^6x=\left(\sin^2x+\cos^2x\right)\left(\sin^4x-\sin^2x\cdot\cos^2x+\cos^4x\right)\\ =\left(\sin^2x+\cos^2x\right)^2-3\sin^2x\cdot\cos^2x=1-\dfrac{3}{4}\sin^22x\)
Do \(0\le\sin^22x\le1\Leftrightarrow\dfrac{3}{4}\cdot0\ge-\dfrac{3}{4}\sin^22x\ge-\dfrac{3}{4}\)
\(\Leftrightarrow1\ge1-\dfrac{3}{4}\sin^22x\ge1-\dfrac{3}{4}=\dfrac{1}{4}\\ \Leftrightarrow\dfrac{4}{3}\ge\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)\ge\dfrac{1}{4}\cdot\dfrac{4}{3}=\dfrac{1}{3}\)
Ta có \(-1\le\cos4x\le1\)
\(\Leftrightarrow\dfrac{1}{3}-1-1\le\dfrac{4}{3}\left(\sin^6x+\cos^6x\right)+\cos4x-1\le\dfrac{4}{3}+1-1\\ \Leftrightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
Vậy \(y_{min}=-\dfrac{5}{3};y_{max}=\dfrac{4}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 9 2021
\(y=\dfrac{4}{3}\left(sin^6x+cos^6x\right)+cos4x-1\)
\(y=\dfrac{4}{3}\left(\dfrac{5}{8}+\dfrac{3}{8}cos4x\right)+cos4x-1\)
\(y=\dfrac{3}{2}cos4x-\dfrac{1}{6}\)
\(-1\le cos4x\le1\Rightarrow-\dfrac{5}{3}\le y\le\dfrac{4}{3}\)
\(y_{min}=-\dfrac{5}{3}\) khi \(cos4x=-1\)
\(y_{max}=\dfrac{4}{3}\) khi \(cos4x=1\)
PT
1
CM
8 tháng 11 2017
sin 6 x + cos 6 x = 4 cos 2 2 x ⇔ sin 2 x + cos 2 x 3 - 3 sin 2 x . cos 2 x ( sin 2 x + cos 2 x ) = 4 cos 2 2 x
PT
1
CM
7 tháng 1 2018
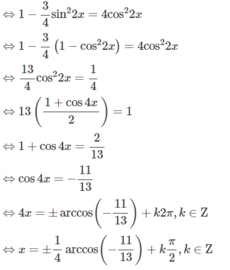
Đáp án: C
Ta có:
sin 6 x + c o s 6 x = ( sin 2 x ) 3 + ( cos 2 x ) 3
= ( sin 2 x + c o s 2 x )( sin 4 x - sin 2 x cos 2 x + c o s 4 x )
= sin 4 x - sin 2 x cos 2 x + c o s 4 x
= ( sin 2 x + cos 2 x ) 2 - 3 sin 2 x cos 2 x
= 1 - 3 sin 2 x cos 2 x
= 1 - (3/4) sin 2 2 x
Vì
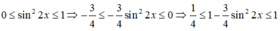
Vậy giá trị nhỏ nhất của sin 6 x + c o s 6 x là 1/4
Dấu “=” xảy ra ⇔ sin 2 2 x = 1 ⇔ sin2x = 1 hoặc sin2x = -1
hình như sai đề