tìm Max: 1) \(\dfrac{2\sqrt{x}}{x+1}\) ; 2)\(\dfrac{\sqrt{x}+4}{\sqrt{x}+2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\left(x\ge0,x\ne1\right)\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right).\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{2}{\sqrt{x}-1}=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)
b) Ta có: \(x\ge0\Rightarrow x+\sqrt{x}+1\ge1\Rightarrow\dfrac{2}{x+\sqrt{x}+1}\le2\)
\(\Rightarrow max=2\) khi \(x=0\)
Ta có: \(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}\)
\(=\dfrac{2}{x+\sqrt{x}+1}\)

a: ĐKXĐ: x>=0; x<>1
\(P=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right)\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}+2}{2}\cdot\dfrac{x-1}{\sqrt{x}+1}\)
\(=-\sqrt{x}\left(\sqrt{x}-1\right)\)
b: 0<x<1
=>căn x<1
=>căn x-1<0
=>căn x*(căn x-1)<0
=>-căn x*(căn x-1)>0
=>P>0
c: \(P=-x+\sqrt{x}-\dfrac{1}{4}+\dfrac{1}{4}\)
\(=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{4}< =\dfrac{1}{4}\)
Dấu = xảy ra khi x=1/4

1. 1/x + 2/1-x = (1/x - 1) + (2/1-x - 2) + 3
= 1-x/x + (2-2(1-x))/1-x + 3
= 1-x/x + 2x/1-x + 3 >= 2√2 + 3
Dấu "=" xảy ra khi x =√2 - 1
2. a = √z-1, b = √x-2, c = √y-3 (a,b,c >=0)
=> P = √z-1 / z + √x-2 / x + √y-3 / y
= a/a^2+1 + b/b^2+2 + c/c^2+3
a^2+1 >= 2a => a/a^2+1 <= 1/2
b^2+2 >= 2√2 b => b/b^2+2 <= 1/2√2
c^2+3 >= 2√3 c => c/c^2+3 <= 1/2√3
=> P <= 1/2 + 1/2√2 + 1/2√3
Dấu = xảy ra khi a^2 = 1, b^2 = 2, c^2 =3
<=> z-1 = 1, x-2 = 2, y-3 = 3
<=> x=4, y=6, z=2

$A=2x-\sqrt{x}=2(x-\frac{1}{2}\sqrt{x}+\frac{1}{4^2})-\frac{1}{8}$
$=2(\sqrt{x}-\frac{1}{4})^2-\frac{1}{8}$
$\geq \frac{-1}{8}$
Vậy $A_{\min}=-\frac{1}{8}$. Giá trị này đạt tại $x=\frac{1}{16}$
$B=x+\sqrt{x}$
Vì $x\geq 0$ nên $B\geq 0+\sqrt{0}=0$
Vậy $B_{\min}=0$. Giá trị này đạt tại $x=0$

a) đk: x\(\ge0\);
P = \(\left[\dfrac{x+2}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}+1}\right].\dfrac{4\sqrt{x}}{3}\)
= \(\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}.\dfrac{4\sqrt{x}}{3}\)
= \(\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}.\dfrac{4\sqrt{x}}{3}=\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}\)
b) Để P = \(\dfrac{8}{9}\)
<=> \(\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}=\dfrac{8}{9}\)
<=> \(\dfrac{\sqrt{x}}{x-\sqrt{x}+1}=\dfrac{2}{3}\)
<=> \(\dfrac{3\sqrt{x}-2x+2\sqrt{x}-2}{3\left(x-\sqrt{x}+1\right)}=0\)
<=> \(-2x+5\sqrt{x}-2=0\)
<=> \(\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\)
<=> \(\left[{}\begin{matrix}x=4\left(tm\right)\\x=\dfrac{1}{4}\left(tm\right)\end{matrix}\right.\)
c)
Đặt \(\sqrt{x}=a\) (\(a\ge0\))
P = \(\dfrac{4a}{3\left(a^2-a+1\right)}\)
Xét P + \(\dfrac{4}{9}\) = \(\dfrac{4a}{3a^2-3a+3}+\dfrac{4}{9}=\dfrac{12a+4a^2-4a+4}{9\left(a^2-a+1\right)}=\dfrac{4a^2+8a+4}{9\left(a^2-a+1\right)}=\dfrac{4\left(a+1\right)^2}{9\left(a^2-a+1\right)}\ge0\)
Dấu "=" <=> a = -1 (loại)
=> Không tìm được Min của P
Xét P - \(\dfrac{4}{3}\) = \(\dfrac{4a}{3\left(a^2-a+1\right)}-\dfrac{4}{3}=\dfrac{4a-4a^2+4a-4}{3\left(a^2-a+1\right)}=\dfrac{-4a^2+8a-4}{3\left(a^2-a+1\right)}=\dfrac{-4\left(a-1\right)^2}{3\left(a^2-a+1\right)}\le0\)
<=> \(P\le\dfrac{4}{3}\)
Dấu "=" <=> a = 1 <=> x = 1 (tm)

\(P=\dfrac{x}{\sqrt{2.\dfrac{1}{2}x+2yz}}+\dfrac{y}{\sqrt{2.\dfrac{1}{2}y+zx}}+\dfrac{z}{\sqrt{2.\dfrac{1}{2}z+xy}}\)
\(=\dfrac{x}{\sqrt{2x\left(x+y+z\right)+yz}}+\dfrac{y}{\sqrt{2y\left(x+y+z\right)+2zx}}+\dfrac{z}{\sqrt{2z\left(x+y+z\right)+2xy}}\)
\(=\dfrac{x}{\sqrt{2\left(x+y\right)\left(x+z\right)}}+\dfrac{y}{\sqrt{2\left(x+y\right)\left(y+z\right)}}+\dfrac{z}{\sqrt{2\left(x+z\right)\left(y+z\right)}}\)
\(=\dfrac{1}{2\sqrt{2}}.2\sqrt{\dfrac{x}{x+y}}.\sqrt{\dfrac{x}{x+z}}+\dfrac{1}{2\sqrt{2}}.2\sqrt{\dfrac{y}{x+y}}.\sqrt{\dfrac{y}{y+z}}+\dfrac{1}{2\sqrt{2}}.2\sqrt{\dfrac{z}{x+z}}.\sqrt{\dfrac{z}{y+z}}\)
\(\le\dfrac{1}{2\sqrt{2}}\left(\dfrac{x}{x+y}+\dfrac{x}{x+z}+\dfrac{y}{x+y}+\dfrac{y}{y+z}+\dfrac{z}{x+z}+\dfrac{z}{y+z}\right)\)
\(=\dfrac{3}{2\sqrt{2}}\)
Dấu "=" xảy ra tại \(x=y=z=\dfrac{1}{6}\)

ĐKXĐ: \(x\ge0\)
Do \(\left\{{}\begin{matrix}2>0\\x+\sqrt{x}+1>0\end{matrix}\right.\) nên \(A_{max}\) khi \(x+\sqrt{x}+1\) đạt GTNN
Mà \(x\ge0\Rightarrow x+\sqrt{x}+1\ge1\)
\(\Rightarrow\dfrac{2}{x+\sqrt{x}+1}\le2\)
Hay \(A_{max}=2\) khi \(x=0\)

Xét A= \(\dfrac{x}{\sqrt{x+2yz}}\).\(\dfrac{1}{\sqrt{2}}\)=\(\dfrac{x}{\sqrt{2x+4yz}}\)=\(\sqrt{\dfrac{x.x}{2x+4yz}}\)
ta có x+y+z=\(\dfrac{1}{2}\)=> 2x+2y+2z= 1=> 2x+4yz= 4yz+1-2y-2z=(2y-1)(2z-1)
từ đó A= \(\sqrt{\dfrac{x}{2y-1}.\dfrac{x}{2z-1}}\)=\(\sqrt{\dfrac{x}{2y-2x-2y-2z}.\dfrac{x}{2z-2x-2y-2z}}\)
=\(\sqrt{\dfrac{x}{-2\left(x+y\right)}\dfrac{x}{-2\left(x+z\right)}}\)=\(\sqrt{\dfrac{1}{4}.\dfrac{x}{x+z}.\dfrac{x}{x+y}}\)=\(\dfrac{1}{2}\sqrt{\dfrac{x}{x+y}.\dfrac{x}{x+z}}\)
Áp dụng cô si \(\sqrt{ab}\)≤\(\dfrac{a+b}{2}\) =>\(\dfrac{1}{2}\sqrt{ab}\)≤\(\dfrac{a+b}{4}\)ta được
A≤\(\dfrac{1}{4}\).(\(\dfrac{x}{x+y}\)+\(\dfrac{x}{x+z}\))
cmmt thì \(\dfrac{P}{\sqrt{2}}\)≤ \(\dfrac{1}{4}\).\(\left(\dfrac{x}{x+y}+\dfrac{x}{x+z}+\dfrac{y}{y+x}+\dfrac{y}{y+z}+\dfrac{z}{z+x}+\dfrac{z}{z+y}\right)\)
\(\dfrac{P}{\sqrt{2}}\)≤\(\dfrac{3}{4}\)=>P≤\(\dfrac{3.\sqrt{2}}{4}\)=\(\dfrac{3}{2\sqrt{2}}\)
Dấu"=" xảy ra <=> x=y=z=\(\dfrac{1}{6}\)
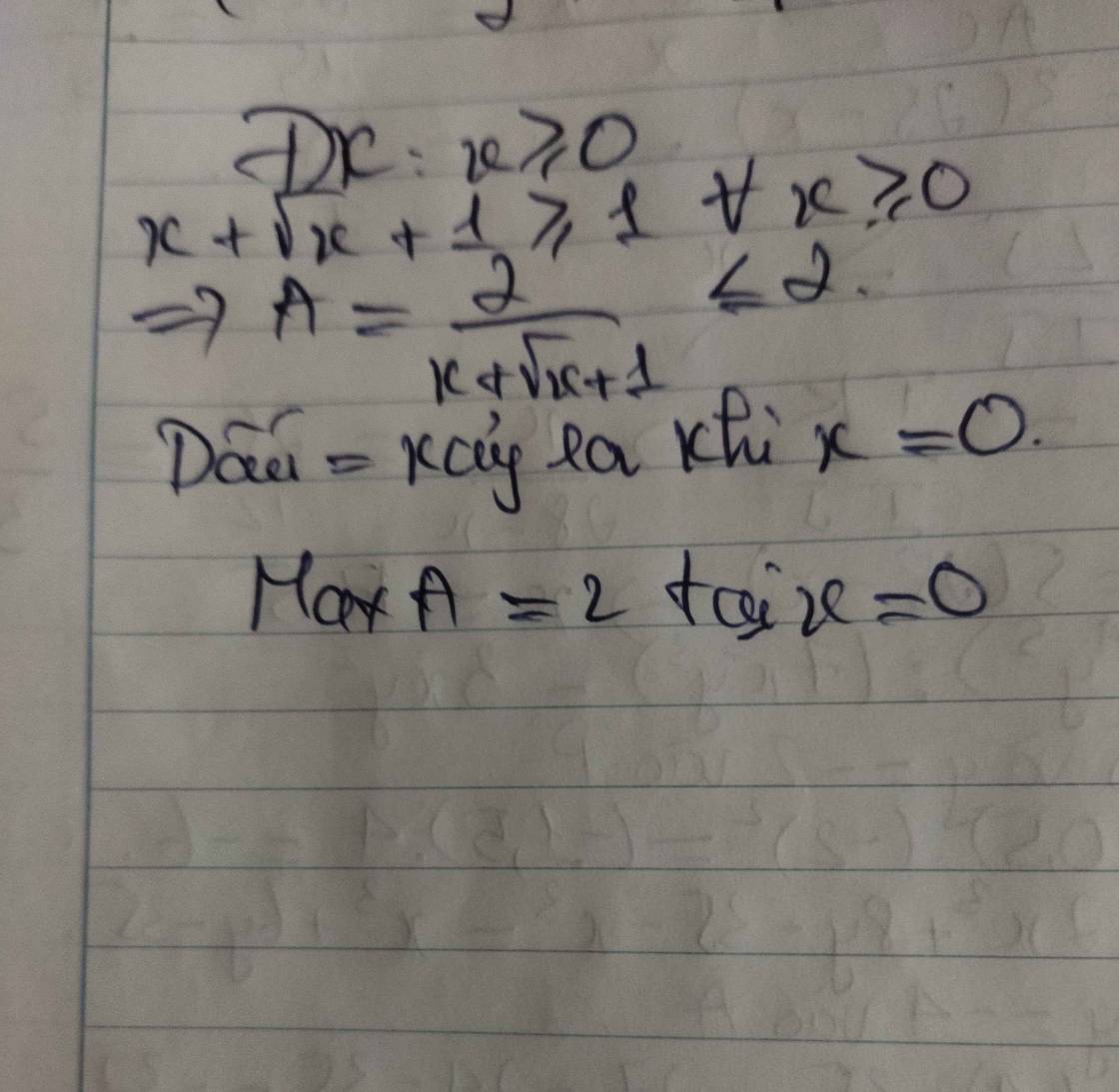
********************************************************
1) ĐK \(x\ge0\)
Ta có: \(\dfrac{2\sqrt{x}}{x+1}=\dfrac{-x+2\sqrt{x}-1+x+1}{x+1}=\dfrac{-\left(\sqrt{x}-1\right)^2}{x+1}+1\)
\(\Leftrightarrow\dfrac{2\sqrt{x}}{x+1}\le1\) (Vì \(\dfrac{-\left(\sqrt{x}-1\right)^2}{x+1}\le0\))
Vậy GTLN của biểu thức này là 1 <=> x=1
2) ĐK \(x\ge0\)
Ta có: \(\dfrac{\sqrt{x}+4}{\sqrt{x}+2}=\dfrac{2\sqrt{x}+4-\sqrt{x}}{\sqrt{x}+2}=2-\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
\(\Leftrightarrow\dfrac{\sqrt{x}+4}{\sqrt{x}+2}\le2\) (Vì \(-\dfrac{\sqrt{x}}{\sqrt{x}+2}\le0\))
Vậy GTLN của biểu thức này là 2 <=> x=0