cho 2 đường thẳng AB song song với CD lấy M thuộc AB; N thuộc CD sao cho 2 tia MB và ND thuộc cùng 1 nửa mặt phẳng bờ MN vẽ tia Mx ở trong góc AMN vẽ tia MY trên nửa mặt phẳng bờ CD ko chứa M sao cho góc AMX=CMY chứng minh mx song song với NY
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C D M N x y
Dpcm ANx // CNy
do AB//CD nen
=>AM // CM va MB//ND
=>AMB // CND
=>ANx // CNy
a). Ta có: góc AMx=góc B (GT)
Mà góc AMx và góc B là hai góc đồng vị.
=> Mx//BC.
Kéo dài tia Mx, cắt CD tại E.
Vì AB//CD(gt) nên AMEˆ=DEMˆ(slt)AME^=DEM^(slt)
mà theo gt AMEˆ=CNyˆAME^=CNy^ nên DEMˆ=CNyˆDEM^=CNy^
=> Mx//Ny(do có 1 cặp góc bằng nhau ở vị trí so le trong
A M x C D

Ta có:AB=AD
=>AC là đường trung tuyến
Mà AG=\(\frac{1}{3}\)AC nên:
=>G là trọng tâm
Ta có:tia DE cắt BC tại E nên:
=>DE là đường trung tuyến
=>BE=EC
Xét ΔDBE và ΔDEF có:
góc D1=góc D2 (so le trong) (DB//EF)
DE cạnh chung
góc FDG=góc E1 (so le trong)
=>ΔDBE=ΔDEF(g.c.g)
=>BE=DF(2 cạnh tương ứng)
Mà BE=EC nên EC=DF
Xét ΔDEM và ΔEMC có:
góc D3=góc C(so le trong) (DF//BE)
góc F=góc E3(so le trong) (DF//BE)
EC=DF (cmt)
=>ΔDEM=ΔEMC (g.c.g)
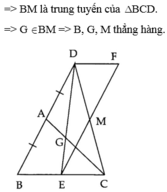
=>DM=MC (2 cạnh tương ứng)
=>BM là đường trung tuyến
=>B,G,M thẳng hàng
CHÚC BN HC TỐT!!!^^