Tính tổng các hệ số của tất cả các hạng tử trong khai triển nhị thức;
a) \(\left(5x-3\right)^6\)
b) \(\left(3x-4y\right)^{20}\)
Vậy đó: Giúp tui nha ^^ Cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QM
0
HH
0
CM
2 tháng 10 2019
Ta có x + 1 x n = ∑ k = 0 n C n k x n - 2 k
Theo đề ta có C n 0 + C n 1 = 24 ⇔ 1 + n = 24 ⇔ n = 23
Số hạng chứa x mũ nguyên dương thỏa n - 2 k > 0 ⇔ k < n 2 = 23 2
Do k ∈ Z nên k ∈ 1 ; 2 ; 3 ; . . 11 .
Suy ra có 12 số hạng chứa x mũ nguyên dương
Đáp án C
PN
3
18 tháng 7 2015
a, Thay x = 1 ta có
a, ( 5.1 - 3)^2 = 2^ 2 = 4
VẬy tổng các hệ số là 4
b thay x = 1 ; y = 1 ta có:
( 3.1 - 4.1 )^20 = (-1)^20 = 1
(*) Tổng quát muố tính tổng các hệ số sau khi khai chuyển ta chỉ việc thay 1 vào
5 tháng 10 2017
mk ko nghĩ như vậy khi khai triển theo pascal kết quả hoàn toàn khác
CM
8 tháng 1 2017
Ta có: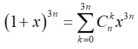 
Chọn x=1. Ta có tổng hệ số bằng: 
Lại có: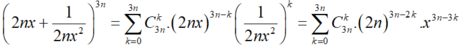 
Số hạng không chứa x suy ra 
Do đó số hạng không chứa x là: 
Chọn D.
HT
12 tháng 12 2020
2/ \(\left(a+b\right)^k\Rightarrow k+1\left(so-hang\right)\)
\(\Rightarrow n+6+1=17\Rightarrow n=10\)
6/ \(\left(2a-1\right)^6=\sum\limits^6_{k=0}C^k_6.2^{6-k}.\left(-1\right)^k.a^{6-k}\)
\(\Rightarrow tong-3-so-hang-dau=C^0_6.2^6+C^1_6.2^5.\left(-1\right)+C^2_6.2^4.\left(-1\right)^2=...\)
7/ \(\left(x-\sqrt{y}\right)^{16}=\left(x-y^{\dfrac{1}{2}}\right)^{16}\)
\(\Rightarrow tong-2-so-hang-cuoi=C^{16}_{16}+C^{15}_{16}=...\)