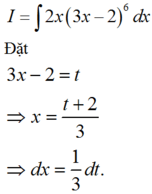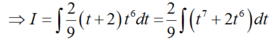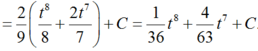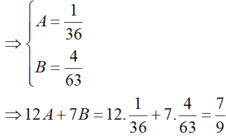A=7a+12a+7b với a+b=40
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NC
Nguyen Cong Minh
30 tháng 9 2017
Đúng(0)
Những câu hỏi liên quan
10 tháng 10 2015
a) \(A=7a+7b=7\left(a+b\right)=7.11=77\)
b) \(B=13a+19b+4a-2b=17a+17b=17\left(a+b\right)=17.100=1700\)
c) \(C=5a-4b+7a-8b=12a-12b=12\left(a-b\right)=12.8=96\)
7 tháng 5 2023
Gọi số cây mà `3` lớp trồng được lần lượt là `x,y,z (x,y,z \in \text {N*})`
Vì số cây của `3` lớp lần lượt tỉ lệ với `3:4:5`
Nghĩa là: `x/3=y/4=z/5`
Số cây trồng được của lớp `7A, 7B` nhiều hơn lớp `7C` là `40` cây
`-> x+y-z=40`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/3=y/4=z/5=(x+y-z)/(3+4-5)=40/2=20`
`-> x/3=y/4=z/5=20`
`-> x=20*3=60, y=20*4=80, z=20*5=100`
Vậy, số cây của `3` lớp lần lượt là `60` cây, `80` cây, `100` cây.
N
7 tháng 5 2023
Gọi số cây trồng được của 3 lớp 7A,7B,7C lần lượt là \(x,y,z\)(cây) \((x,y,z \in N*)\)
Do số cây trồng được của 3 lớp 7A,7B,7C lần lượt tỉ lệ với 3,4,5 nên:\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Do số cây trồng được của 2 lớp 7A,7B nhiều hơn số cây trồng được của lớp 7C là 40 cây nên \(x+y-z=40\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y-z}{3+4-5}=\dfrac{40}{2}=20\)
Do đó:
\(\dfrac{x}{30}=20\Rightarrow x=60\)
\(\dfrac{y}{4}=20\Rightarrow y=80\) \(\left(TM\right)\)
\(\dfrac{z}{5}=20\Rightarrow z=100\)
NV
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
9 tháng 11 2018
\(\frac{a}{b}=\frac{c}{d}=\frac{7a}{7b}=\frac{2c}{2d}=\frac{7a+2c}{7b+2d}\left(1\right)\) (Tính chất dãy tỷ số bằng nhau)
\(\frac{a}{b}=\frac{c}{d}=\frac{7a}{7b}=\frac{2c}{2d}=\frac{7a-2c}{7b-2d}\left(2\right)\) (lý do như trên)
Từ (1) và (2) \(\Rightarrow\frac{7a+2c}{7b+2d}=\frac{7a-2c}{7b-2d}\)
TT
1