Chứng minh rằng trong chuyển động biến đổi đều hiệu các số quãng đường đi trong hai khoảng thời gian liên tiếp bằng nhau là một hằng số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng công thức tính đường đi s = 1 2 a t 2 ta được:
s 1 = 1 2 a t 2 ; s 2 = 1 2 a 2 t 2 = 4 2 a t 2 ; s 3 = 1 2 a 3 t 2 = 9 2 a t 2 ... ;
s n − 1 = 1 2 a n − 1 t 2 a t 2 ; s n = 1 2 a n t 2 = n 2 2 a t 2 .
Do đó Δ s 1 = s 1 − 0 = 1 2 a t 2 ; Δ s 2 = s 2 − s 1 = 3 2 a t 2 ; Δ s 3 = s 3 − s 2 = 5 2 a t 2 ... ;
Δ s n = s n − s n − 1 = 1 2 n 2 − n − 1 2 a t 2 = 2 n − 1 2 a t 2 .
Suy ra Δ s 2 Δ s 1 = 3 ; Δ s 3 Δ s 1 = 5 ; ... ; Δ s n Δ s 1 = 2 n − 1 .
Từ đó suy ra Δ s 1 : Δ s 2 : Δ s 3 : ... = 1 : 3 : 5 : ...

Gia tốc của vật là:
\(s=\dfrac{1}{2}at^2\)
\(\Rightarrow a=\dfrac{2s}{t^2}=\dfrac{2\cdot0,9}{1,5^2}=0,8\left(m/s^2\right)\)

Chọn đáp án C
Lời giải:
+ Chọn chiều dương là chiều chuyển động, gốc thời gian là lúc xuất phát, gốc tọa độ tại vị trí xuất phát với
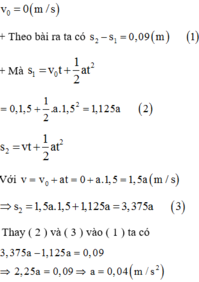


Giải : Chọn chiều dương là chiều chuyển động, gốc thời gian là lúc xuất phát, gốc tọa độ tại vị trí xuất phát với v 0 = 0 m / s
Theo bài ra ta có s 2 − s 1 = 0 , 09 m 1
Mà s 1 = v 0 t + 1 2 a t 2 = 0 , 1 , 5 + 1 2 . a .1 , 5 2 = 1 , 125 a 2
s 2 = v t + 1 2 a t 2
Với v = v 0 + a t = 0 + a .1 , 5 = 1 , 5 a m / s
⇒ s 2 = 1 , 5 a .1 , 5 + 1 , 125 a = 3 , 375 a 3
Vậy lực tác dụng lên vật F = m a = 0 , 15.0 , 04 = 0 , 06 N

đáp án của bài này là C. 5m/s^2
S1= vot + at^2/2=12 <=> S1= vo.2 + 2a= 12
S12= vot + at^2/2= S1 +S2= 44 <=> vo4 + 8a = 44
Giải hệ ta đc a= 2,5m/s^2
vo=1m/s

sửa đề 1 chút
Chứng tỏ rằng trong chuyển đọng thẳng nhanh dần đều không có vận tốc đầu, quãng đường đi được trong những khoảng thời gian bằng nhau liên tiếp tỉ lệ với các số lẻ liên tiếp 1,3,5…
Giải:
Áp dụng công thức tính đường đi : \(s=\dfrac{1}{at^2}\)
Ta có: \(s_1=\dfrac{1}{2}at^2;s_2=\dfrac{1}{2}a\left(2t\right)^2=\dfrac{4}{2}at^2;s_3=\dfrac{9}{2}at^2...\)
\(s_{n-1}=\dfrac{1}{2}a\left[\left(n-1\right)t\right]^2=\dfrac{\left(n-1\right)^2}{2}at^2;s_n=\dfrac{1}{2}a\left(nt\right)^2=\dfrac{n^2}{2}at^2\)
\(\Delta s_1=s_1-0=\dfrac{1}{2}at^2;\Delta s_2=s_1-s_2=\dfrac{3}{2}at^2;\Delta s_3=s_{3-}s_2=\dfrac{5}{2}at^2....\)
$\Delta s_n=s_{n-1}-s_n=\dfrac{1}{2}\left[n^2-\left(n-1\right)^2\right]at^2=\dfrac{2n-1}{2}at^2$
$\Rightarrow\dfrac{\Delta s_2}{\Delta s_1}=3;\dfrac{\Delta s_3}{\Delta s_1}=5...;\dfrac{\Delta s_n}{\Delta s_{n-1}}=2n-1$
Tức là $\Delta s_1;\Delta s_2;\Delta s_3...=1,3,5,..$
nn