Giúp mình với tks ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 3 2022
\(\text{Δ}=\left(-2m\right)^2-4\left(m^2-m-2\right)\)
\(=4m^2-4m^2+4m+8\)
=4m+8
Để phương trình có hai nghiệm thì 4m+8>=0
hay m>=-2
Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\left(-2m\right)^2-2\left(m^2-m-2\right)=4\)
\(\Leftrightarrow4m^2-2m^2+2m=0\)
=>2m(m+1)=0
=>m=0 hoặc m=-1
6 tháng 5 2022
Câu 15)
Theo đề bài
\(m_1+m_2=20\)
Ta có phương tình cân bằng nhiệt
\(Q_{toả}=Q_{thu}\\ \Leftrightarrow m_14200\left(100-30\right)=20-m_1.4200\left(30-15\right)\\ \Rightarrow\left\{{}\begin{matrix}m_1=3,5\\m_2=20-m_1=16,4\end{matrix}\right.\)
Câu 16)
Ta có phương trình cân bằng nhiệt
\(Q_{toả}=Q_{thu}\\ \Leftrightarrow0,6.380\left(100-t_{cb}\right)=2,5.4200\left(t_{cb}-20\right)\\ \Rightarrow t_{cb}=21,7^o\)
PS
1
28 tháng 8 2021
\(\dfrac{1.2}{0.8}=\dfrac{3.6}{3x}\)
\(\Leftrightarrow3\cdot x=2.4\)
hay x=0,8
N
20 tháng 10 2021
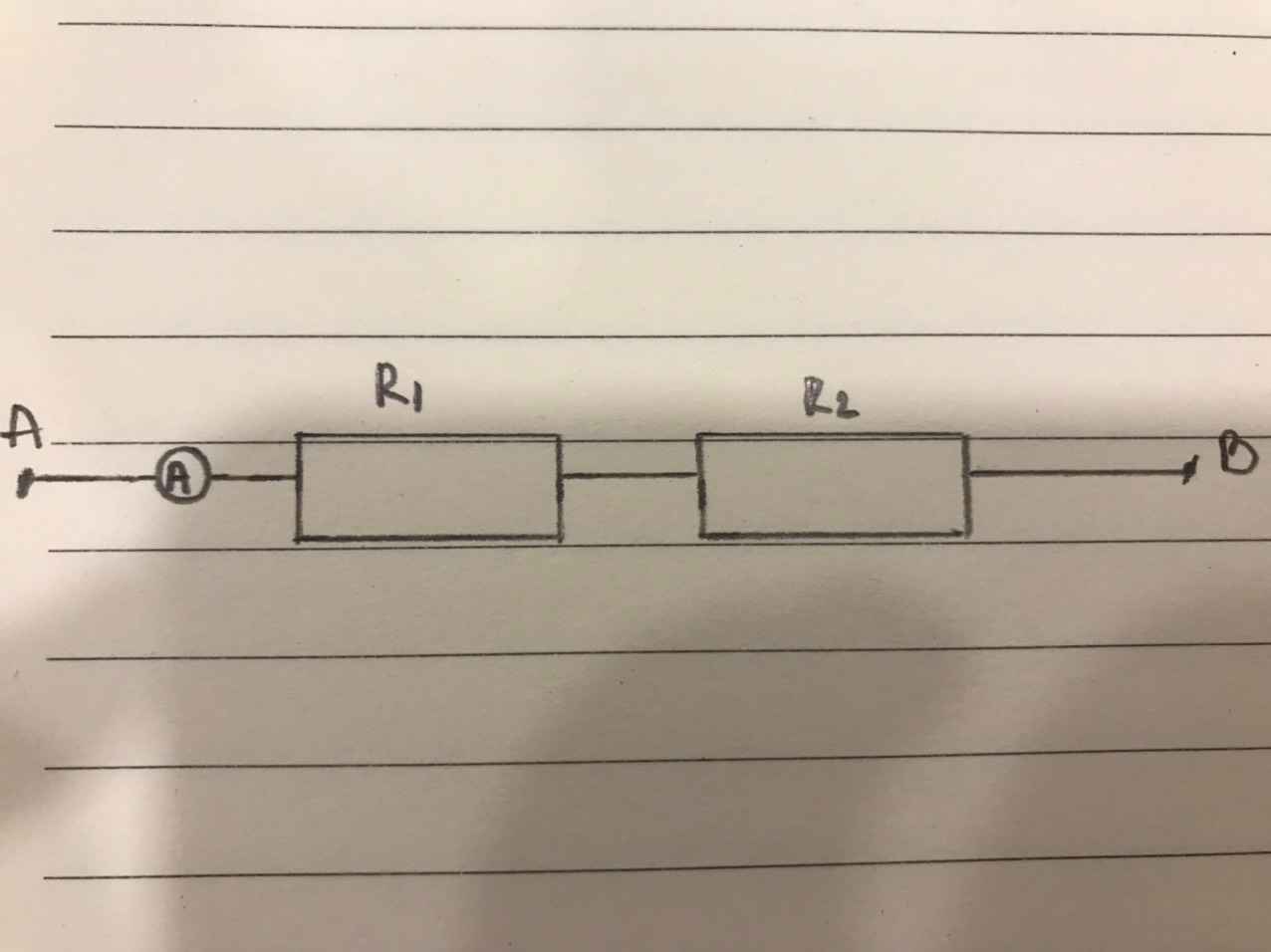
Bài 1:
\(R=R1+R2=30+80=110\Omega\)
\(I=I1=I2=U:R=110:110=1A\left(R1ntR2\right)\)
\(\left\{{}\begin{matrix}U1=R1.I1=30.1=30V\\U2=R2.I2=80.1=80V\end{matrix}\right.\)
Bài 2:
a. \(R=R1+R2+R3=4+4+4=12\Omega\)
b. \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(4+4\right)4}{4+4+4}=\dfrac{8}{3}\Omega\)
19 tháng 7 2018
a) Đặt A = I 2x-1/3 I +107
Có I 2x - 1/3 I \(\ge\)0 với mọi x
=> I 2x - 1/3 I + 107 \(\ge\)107 với mọi x
Để A đạt GTNN thì A = 107
Dấu " = " xảy ra \(\Leftrightarrow\)I 2x-1/3 I = 0
\(\Leftrightarrow\)2x - 1/3 = 0
\(\Leftrightarrow\) 2x = 1/3
\(\Leftrightarrow\) x = 1/6
=> KL
b) Đặt B = I 1 - 4x I -1
Có I 1 - 4x I \(\ge\)0 với mọi x
\(\Rightarrow\)I 1 - 4x I - 1 \(\ge\)-1 với mọi x
Để B đạt GTNN thì B = -1
Dấu " = " xảy ra \(\Leftrightarrow\)I 1 - 4x I = 0
\(\Leftrightarrow\) 1 - 4x = 0
\(\Leftrightarrow\) 4x = 1
\(\Leftrightarrow\) x = 1/4
=> KL
NH
1
DD
Đoàn Đức Hà
Giáo viên
24 tháng 8 2021
\(cos\alpha=\frac{1}{2}\Leftrightarrow\alpha=\frac{-\pi}{3}\)(vì \(\frac{-\pi}{2}< \alpha< 0\))
\(cot\left(\frac{\pi}{3}-\alpha\right)=cot\left(\frac{2\pi}{3}\right)=\frac{-\sqrt{3}}{3}\)
\(B=\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}\right):\left(1-\dfrac{1}{\sqrt{x}-1}\right)=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-3\right)-\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)+3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}:\dfrac{\sqrt{x}-1-1}{\sqrt{x}-1}=\dfrac{x-\sqrt{x}-6-x+1+3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}.\)
\(\dfrac{\sqrt{x}-1}{\sqrt{x}-2}=\dfrac{2\sqrt{x}-6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}.\dfrac{\sqrt{x}-1}{\sqrt{x}-2}=\dfrac{2\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{2}{\sqrt{x}-2}\)
Để B=3 thì \(\dfrac{2}{\sqrt{x}-2}=3\left(ĐKXĐ:x\ge0.và.x\ne4\right)\)
Đến đây tự giải tiếp nhé