
giúp em câu 12,13 em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


71.
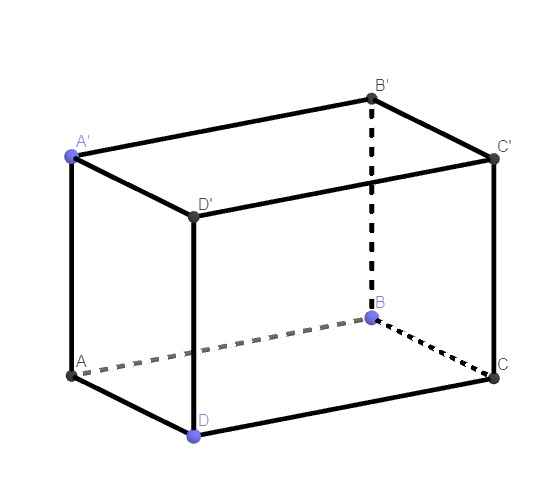
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)


a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
Suy ra: DE⊥BC

Câu 15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=\dfrac{a-b+c}{2-3+5}=\dfrac{-10.2}{4}=-2.55\)
Do đó: a=-5,1; b=-7,65; c=-12,75


Câu 3:
BPTT: so sánh
Tác dụng: Cho thấy tầm quan trọng của mọi người trong thời kì dịch bệnh và lời nhắc nhở các lương y phải luôn giúp đỡ người bệnh, yêu thương và coi như người nhà

2.
Áp dụng định lý hàm cosin:
\(b=\sqrt{a^2+c^2-2ac.cosB}=\sqrt{8^2+3^2-2.8.3.cos60^0}=7\)
\(S_{ABC}=\dfrac{1}{2}ac.sinB=\dfrac{1}{2}.8.3.sin60^0=6\sqrt{3}\)
4.
\(\Delta=\left(m+2\right)^2-16>0\Leftrightarrow m^2+4m-12>0\Rightarrow\left[{}\begin{matrix}m>2\\m< -6\end{matrix}\right.\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m-2\\x_1x_2=4\end{matrix}\right.\)
\(x_1+x_2+x_1x_2>1\)
\(\Leftrightarrow-m-2+4>1\)
\(\Rightarrow m< 1\) (2)
Kết hợp (1); (2) ta được \(m< -6\)

b: Ta có: \(\dfrac{4}{\sqrt{3}+1}+\dfrac{5}{2-\sqrt{3}}-\dfrac{6}{3-\sqrt{3}}\)
\(=2\sqrt{3}-2+10-5\sqrt{3}-3-\sqrt{3}\)
\(=-4\sqrt{3}+5\)

1 He doesn't play games
2 I don't go to the art club
3 What about sitting down?
4 We are going to take part in the stamp collector's club
5 How about relaxing?
6 My favorite subject is English
7 My favorite sport is football
8 Pink and blue are my favorite colors
9 My favorite subject is English
10 My favorite sport is football
\(a,=\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{x-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
Với \(x=28-6\sqrt{3}tmđk\)thay vào P ta có :
\(P=\dfrac{\sqrt{28-6\sqrt{3}}}{28-6\sqrt{3}+\sqrt{28-6\sqrt{3}}+1}=\dfrac{\sqrt{\left(3\sqrt{3}-1\right)^2}}{29-6\sqrt{3}+\sqrt{\left(3\sqrt{3}-1\right)^2}}=\dfrac{3\sqrt{3}-1}{29-6\sqrt{3}+3\sqrt{3}-1}=\dfrac{3\sqrt{3}-1}{28-3\sqrt{3}}=\dfrac{\left(3\sqrt{3}-1\right)\left(28+3\sqrt{3}\right)}{784-27}=\dfrac{81\sqrt{3}-1}{757}\)
\(=\left[\dfrac{1+\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}-\dfrac{1-\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\right]\cdot\dfrac{1-\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\cdot\dfrac{1-\sqrt{a}}{\sqrt{a}}=\dfrac{2}{\sqrt{a}+1}\)
Với \(a=3-2\sqrt{2}tmđk\)thay vào M ta được :
\(M=\dfrac{2}{\sqrt{3-2\sqrt{2}}+1}=\dfrac{2}{\sqrt{\left(\sqrt{2}-1\right)^2}+1}=\dfrac{2}{\sqrt{2}-1+1}=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
Ta có : \(18M=18\cdot\dfrac{2}{\sqrt{a}+1}=\dfrac{36}{\sqrt{a}+1}\)
Đặt \(\dfrac{36}{\sqrt{a}+1}=x^2\left(x\in N\cdot\right)\Rightarrow x^2\left(\sqrt{a}+1\right)=36\)
Ta lại có a2.b2 = (a.b)2 => \(\left\{{}\begin{matrix}x^2\\\sqrt{a}+1\end{matrix}\right.\)phải là bình phương của các số tự nhiên
mà \(x^2\left(\sqrt{a}+1\right)=36\)=> Ta có các trường hợp sau :
\(\left\{{}\begin{matrix}x^2=1\\\sqrt{a}+1=36\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\a=1225\end{matrix}\right.\)(tm)
\(\left\{{}\begin{matrix}x^2=36\\\sqrt{a}+1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\a=0\end{matrix}\right.\)(ktm)
\(\left\{{}\begin{matrix}x^2=4\\\sqrt{a}+1=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\a=64\end{matrix}\right.\)(tm)
\(\left\{{}\begin{matrix}x^2=9\\\sqrt{a}+1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\a=9\end{matrix}\right.\)(tm)