bài 1 khai triển (x-2)^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
3 tháng 8 2023
\(a,\left(x+2\right)^2=x^2+4x+4\\ b,\left(x-1\right)^2=x^2-2x+1\\ c,\left(x^2+y^2\right)^2=x^4+2x^2y^2+y^4\)
KV
20 tháng 8 2023
a) (x - 1/2x²y)²
= x² - 2x . 1/2 x²y + (1/2x²y)²
= x² - x³y + 1/4 x⁴y²
b) (2xy² - 1)(1 + 2xy²)
= (2xy²)² - 1²
= 4x²y⁴ - 1
c) (x - y + 2)²
= (x - y)² + 2(x - y).2 + 2²
= x² - 2xy + y² + 4x - 4y + 4
= x² + y² - 2xy + 4x - 4y + 4
d) (x + 1/2)(1/2 - x)
= (1/2)² - x²
= 1/4 - x²
e) (x² - 1/3)²
= (x²)² - 2x².1/3 + (1/3)²
= x⁴ - 2/3 x² + 1/9
T
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 11 2021
SHTQ: \(C_{10}^k.2^k.x^{10-k}\) có hệ số: \(a_k=C_{10}^k2^k\)
Hệ số lớn nhất khi thỏa mãn:
\(\left\{{}\begin{matrix}a_k\ge a_{k+1}\\a_k\ge a_{k-1}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}C_{10}^k2^k\ge C_{10}^{k+1}2^{k+1}\\C_{10}^k2^k\ge C_{10}^{k-1}2^{k-1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10!}{k!\left(10-k\right)!}\ge\dfrac{10!}{\left(k+1\right)!\left(10-\left(k+1\right)\right)!}.2\\\dfrac{10!}{k!\left(10-k\right)!}.2\ge\dfrac{10!}{\left(k-1\right)!\left(10-\left(k-1\right)\right)!}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{10-k}\ge\dfrac{2}{k+1}\\\dfrac{2}{k}\ge\dfrac{1}{11-k}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}k\ge\dfrac{19}{3}\\k\le\dfrac{22}{3}\end{matrix}\right.\) \(\Rightarrow k=7\)
Hệ số lớn nhất: \(C_{10}^7.2^7\)
KV
9 tháng 7 2023
a) (x² + 2)²
= (x²)² + 2.x².2 + 2²
= x⁴ + 4x² + 4
b) (x + y + z)²
= [(x + y) + z]²
= (x + y)² + 2(x + y).z + z²
= x² + 2xy + y² + 2xz + 2yz + z²
= x² + y² + z² + 2xy + 2xz + 2yz
HT
12 tháng 12 2020
15/ Mũ 4=> có 4+1=5 số hạng=> số hạng chính giữa là: \(C^2_4.3^{4-2}.x^2.2^2y^2=58x^2y^2\)
18/ \(x.x^k=x^7\Rightarrow k=6\)
\(C^6_9.3^6.2^3=489888\)
19/ \(C^7_7+C^7_8.\left(-1\right)^7+C^7_9.2^2=...\)
13 tháng 12 2020
C18 , c19 là lm sao vậy ạ ? Mk ko hiểu 2 bài này nơi
TH
0
T
23 tháng 9 2023
Bài 1.
\(a, (3x-4)^2\)
\(=\left(3x\right)^2-2\cdot3x\cdot4+4^2\)
\(=9x^2-24x+16\)
\(b,\left(1+4x\right)^2\)
\(=1^2+2\cdot1\cdot4x+\left(4x\right)^2\)
\(=16x^2+8x+1\)
\(c,\left(2x+3\right)^3\)
\(=\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot3+3\cdot2x\cdot3^2+3^3\)
\(=8x^3+36x^2+54x+27\)
\(d,\left(5-2x\right)^3\)
\(=5^3-3\cdot5^2\cdot2x+3\cdot5\cdot\left(2x\right)^2-\left(2x\right)^3\)
\(=125-150x+60x^2-8x^3\)
\(e,49x^2-25\)
\(=\left(7x\right)^2-5^2\)
\(=\left(7x-5\right)\left(7x+5\right)\)
\(f,\dfrac{1}{25}-81y^2\)
\(=\left(\dfrac{1}{5}\right)^2-\left(9y\right)^2\)
\(=\left(\dfrac{1}{5}-9y\right)\left(\dfrac{1}{5}+9y\right)\)
Bài 2.
\(a,\left(x-5\right)^2-\left(x+7\right)\left(x-7\right)=8\)
\(\Rightarrow x^2-2\cdot x\cdot5+5^2-\left(x^2-7^2\right)=8\)
\(\Rightarrow x^2-10x+25-\left(x^2-49\right)=8\)
\(\Rightarrow x^2-10x+25-x^2+49=8\)
\(\Rightarrow\left(x^2-x^2\right)-10x=8-25-49\)
\(\Rightarrow-10x=-66\)
\(\Rightarrow x=\dfrac{33}{5}\)
\(b,\left(2x+5\right)^2-4\left(x+1\right)\left(x-1\right)=10\)
\(\Rightarrow\left(2x\right)^2+2\cdot2x\cdot5+5^2-4\left(x^2-1^2\right)=10\)
\(\Rightarrow4x^2+20x+25-4x^2+4=10\)
\(\Rightarrow\left(4x^2-4x^2\right)+20x=10-25-4\)
\(\Rightarrow20x=-19\)
\(\Rightarrow x=\dfrac{-19}{20}\)
#\(Toru\)
KV
23 tháng 9 2023
Bài 1
a) (3x - 4)²
= (3x)² - 2.3x.4 + 4²
= 9x² - 24x + 16
b) (1 + 4x)²
= 1² + 2.1.4x + (4x)²
= 1 + 8x + 16x²
c) (2x + 3)³
= (2x)³ + 3.(2x)².3 + 3.2x.3² + 3³
= 8x³ + 36x² + 54x + 27
d) (5 - 2x)³
= 5³ - 3.5².2x + 3.5.(2x)² - (2x)³
= 125 - 150x + 60x² - 8x³
e) 49x² - 25
= (7x)² - 5²
= (7x - 5)(7x + 5)
f) 1/25 - 81y²
= (1/5)² - (9y)²
= (1/5 - 9y)(1/5 + 9y)
2 tháng 1 2022
Bài 9:
uses crt;
var x,y,n:integer;
begin
clrscr;
readln(n);
x:=0;
y:=0;
while (x*x+y*y<>n) do
begin
x:=x+1;
y:=y+1;
end;
writeln(x,' ',y);
readln;
end.
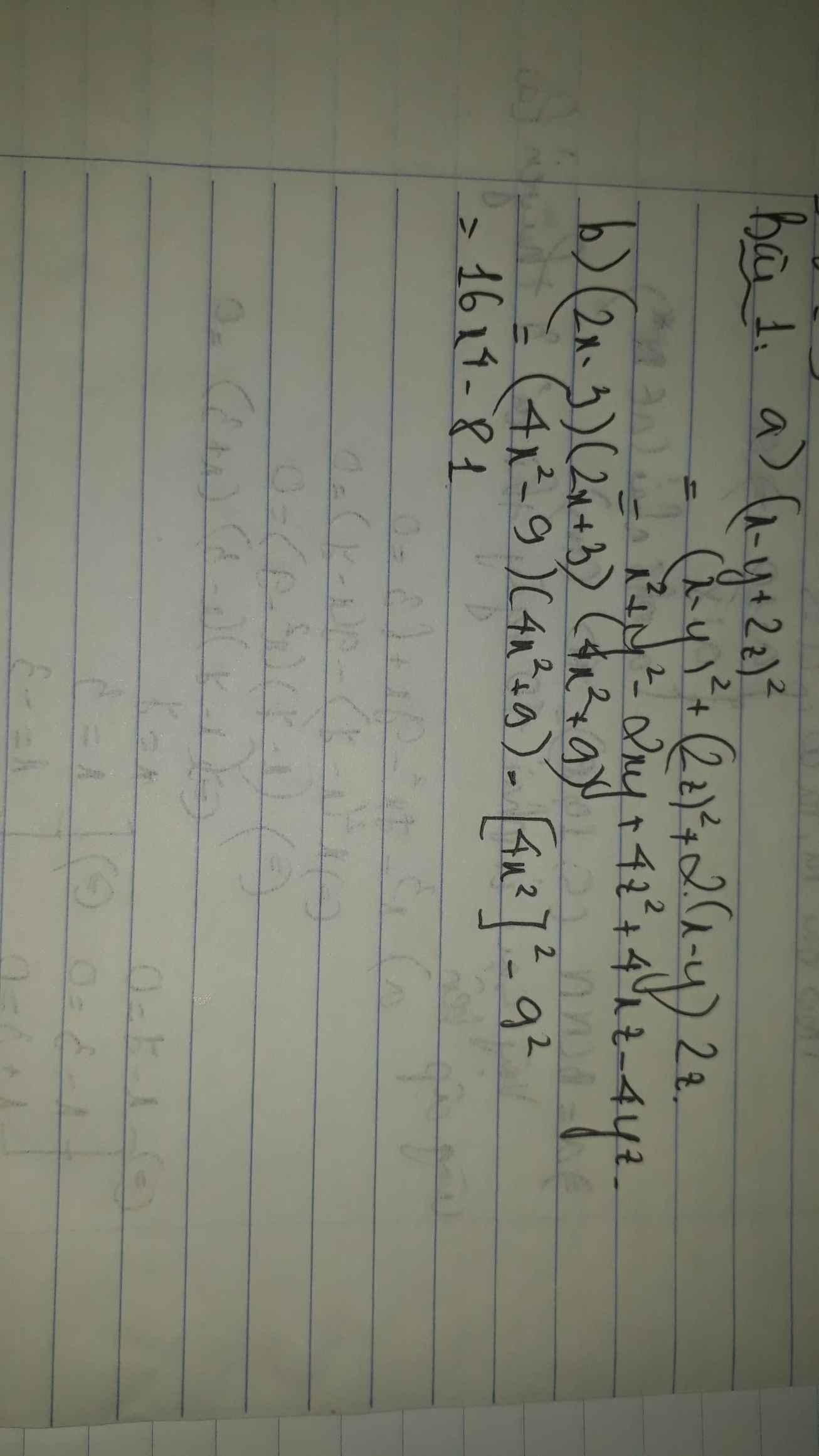
\(\left(x-2\right)^2=x^2-2.x.2+2^2=x^2-4x+4.\)
\(\left(x-2\right)^2=x^2-4x+4\)