Giải phương trình lượng giác:
Tan2 x +cos2 x +cosx +1/cosx =0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hướng dẫn giải
Chọn B.
Ta có : cos2 x- cosx = 0 ó cosx. ( cosx – 1) = 0
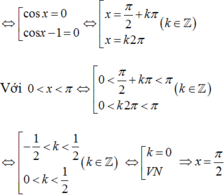

Đáp án B.
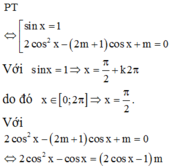
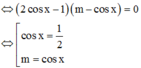
PT: cos x = 1 2 có 2 nghiệm thuộc trên đoạn 0 ; 2 π do đó để PT đã cho có 4 nghiệm thực thuộc đoạn 0 ; 2 π thì
TH1: m= cosx có 1 nghiệm thuộc đoạn 0 ; 2 π
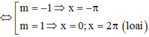
TH2: m= cosx có 2 nghiệm thuộc đoạn 0 ; 2 π trong đó có 1 nghiệm trùng
![]()
Vậy m= -1; m=0.

ĐK: \(x\ne\dfrac{\pi}{6}+k2\pi;x\ne\dfrac{5\pi}{6}+k2\pi\)
\(\dfrac{cosx-\sqrt{3}sinx}{sinx-\dfrac{1}{2}}=0\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=0\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=0\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
Đối chiếu điều kiện ta được \(x=-\dfrac{5\pi}{6}+k2\pi\).

Đáp án A
Phương pháp: Giải phương trình lượng giác sau đó kết hợp vào điều kiện của đầu bài để tìm ra nghiệm thỏa mãn.
Cách giải:
cos 2 x − cos x = 0
⇔ cos x cos x − 1 = 0
⇔ cos x = 0 cos x = 1
⇔ x = π 2 + k π x = 2 k π , k ∈ ℤ
+) Với: x = π 2 + k π : 0 < x < π ⇔ 0 < π 2 + k π < π ⇔ − π 2 < k 2 π < π 2 ⇔ − 1 4 < k < 1 4
Mà k ∈ ℤ nên k = 0 khi đó ta có x = π 2
+) Với: x = 2 k π : 0 < x < π ⇔ 0 < 2 k π < π ⇔ 0 < k < 1 2
Mà k ∈ ℤ nên không có giá trị k nào thỏa mãn.

a: \(\sqrt{3^2+2^2}=\sqrt{13}\)
Chia hai vế cho căn 13, ta được:
\(\dfrac{3}{\sqrt{13}}\cdot\sin2x+\dfrac{2}{\sqrt{13}}\cdot\cos2x=\dfrac{3}{\sqrt{13}}\)
Đặt \(\cos a=\dfrac{3}{\sqrt{13}}\)
Ta được phương trình: \(\sin\left(2x+a\right)=\cos a=\sin\left(\dfrac{\Pi}{2}-a\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+a=\dfrac{\Pi}{2}-a+k2\Pi\\2x+a=\dfrac{\Pi}{2}+a+k2\Pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\left(\dfrac{\Pi}{2}-2a+k2\Pi\right)\\x=\dfrac{\Pi}{4}+k\Pi\end{matrix}\right.\)
b: \(\Leftrightarrow cos^2x-sin^2x+cosx-sinx=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos x=\cos\left(\dfrac{\Pi}{2}-x\right)\\\sin\left(x-\dfrac{\Pi}{4}\right)=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{2}-x+k2\Pi\\x=-\dfrac{\Pi}{2}+x+k2\Pi\\x-\dfrac{\Pi}{4}=-\dfrac{\Pi}{2}+k2\Pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{4}+k\Pi\\x=-\dfrac{\Pi}{4}+k2\Pi\end{matrix}\right.\)