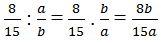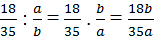Tìm phân số \(\dfrac{a}{b}\) lớn nhất sao cho khi chia mỗi phân số \(\dfrac{12}{35};\dfrac{8}{21};\dfrac{52}{91}\) cho \(\dfrac{a}{b}\) ta đều được một số tự nhiên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 4 2018
Gọi phân số lớn nhất cần tìm là a/b
Ta có: 
Theo đề bài thì 8b/15a là số nguyên nên 8b ⋮ 15a
Mà UCLN(8; 15) = 1 và UCLN(a; b) = 1 nên 8 ⋮ a và b ⋮ 15 (1)
Ta lại có :
Tương tự 18b ⋮ 35a
Mà UCLN(18: 35) = 1 và UCLN(a , b) = 1 nên 18⋮ a và b ⋮ 35 (2)
Từ (1), (2) suy ra : a ∈ UC(8; 18) = {0,1,2}
b ∈ UC(15; 35) = {0,105; 210; …}
Vì a/b lớn nhất nên a lớn nhất, b nhỏ nhất khác 0
Vậy phân số cần tìm là 2/105
HD
1 tháng 5 2018
Gọi phân số lớn nhất cần tìm là a/b
Ta có:
Theo đề bài thì 8b/15a là số nguyên nên 8b ⋮ 15a
Mà UCLN(8; 15) = 1 và UCLN(a; b) = 1 nên 8 ⋮ a và b ⋮ 15 (1)
Ta lại có :
Tương tự 18b ⋮ 35a
Mà UCLN(18: 35) = 1 và UCLN(a , b) = 1 nên 18⋮ a và b ⋮ 35 (2)
Từ (1), (2) suy ra : a ∈ UC(8; 18) = {0,1,2}
b ∈ UC(15; 35) = {0,105; 210; …}
Vì a/b lớn nhất nên a lớn nhất, b nhỏ nhất khác 0
Vậy phân số cần tìm là 2/105
KT
16 tháng 8 2017
12/35 : a/b = 12b / 35a = x 8/21 : a/b = 8b / 21a = y 52/91 : a/b = 52b / 91a = z ==> x= 10y/9 = 5z/3 3 phân số trên chia cho a/b đc các số tự nhiên là x,y,z thì x,y,z >= 1 theo bđt Cosi: (a+b)/2 = căn bậc 2 của (ab) <==> a + b = 2 x (căn bậc 2 của (ab)) (chia 2 vế cho b) <==> a/b + 1 = 2 x (căn bậc 2 của (a/b) biểu thức này lớn nhất khi a lớn nhất, b nhỏ nhất ==> b = 2 ==> 8x2 / 21a = 9x/10 ( do x = 10y/9) 52x2 / 91a = 3x/5 ( do x = 5z/3) hệ trên vô nghiệm nên chắc chắn sẽ ko có phân số a/b nào chia cho 3 phân số đề cho sẽ đc 1 số tự nhiên . Mong bạn hiểu !!!