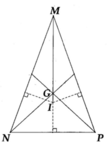
m nằm trong tam gáic đều ABC trọng tâm G ( M#G) . MG cắt AB , BC , CA lần lượt tại C, , A, , B,
Chứng minh rằng : \(\dfrac{MA^,}{GA^,}\) + \(\dfrac{MB^,}{GB^,}\) + \(\dfrac{MC^,}{GC^,}\) =3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

I nằm trong tam giác và cách đều ba cạnh của tam giác nên MI là tia phân giác của góc M.
Do tam giác MNP cân tại M nên đường giác MI cũng là đường trưng tuyến.
G là trọng tâm của tam giác MNP nên G nằm trên MI.
Từ đó, suy ra M,G, I thẳng hàng.

Xét tam giác ABC cân tại A có:
G là trọng tâm
=> G là giao của 3 đường trung tuyến
=>AG là đường trung tuyến
Mà tam giác ABC cân tại A
=>AG cũng là đường trung trực
Mà AI là đường trung trực(do I cách đều 3 điểm)
=>AG trùng AI(Tiên đề Ơ clit)
=>A,G,I thẳng hàng
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà 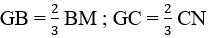
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của
Vì G, I cùng thuộc tia phân giác của 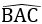

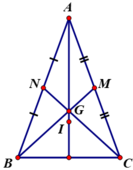
- Gọi M, N là trung điểm CA và BA.
ΔABC cân tại A có BM, CN là đường trung tuyến ứng với cạnh AC, AB.
⇒ BM = CN ( chứng minh ở bài 26)
Mà 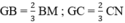 (Tính chất trọng tâm của tam giác)
(Tính chất trọng tâm của tam giác)
⇒ GB = GC
- ΔAGB và ΔAGC có
AG chung
AB = AC (do ΔABC cân tại A)
GB = GC (chứng minh trên)
⇒ ΔAGB = ΔAGC (c.c.c)
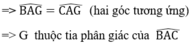
- Theo đề bài I cách đều ba cạnh của tam giác
Dựa vào chứng minh bài 36 ⇒ I là điểm chung của ba đường phân giác
⇒ I thuộc tia phân giác của 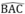
Vì G, I cùng thuộc tia phân giác của 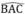 nên A, G, I thẳng hàng
nên A, G, I thẳng hàng

Gọi giao điểm của BG với AC là M;
CG với AB là N
Vì G là trọng tâm của ∆ ABC
nên BM, CN, là trung tuyến
Mặt khác ∆ABC cân tại A
Nên BM = CN
Ta có GB = BM; GC = CN (t/c trọng tâm của tam giác)
Mà BM = CN nên GB = GC
Do đó: ∆AGB = ∆AGC (c.c.c)
=> => G thuộc phân giác của
Mà ∆ABI = ∆ACI (c.c.c)
=> => I thuộc phân giác của
Vì G, I cùng thuộc phân giác của nên A, G, I thẳng hàng


Gọi H, K lần lượt là trung điểm của BC, C'A'
\(\Delta A'BC'\)cân tại B có \(\widehat{A'BC'}=120^0\)\(\Rightarrow\widehat{BC'A'}=\widehat{BA'C'}=30^0\)
\(\Rightarrow\Delta BKC'\)là nửa tam giác đều
\(\Rightarrow BK=\frac{1}{2}BC'\)(1)
\(AH\perp BC\)(do \(\Delta ABC\)đều) nên \(\Delta ABH\)là nửa tam giác đều
\(\Rightarrow BH=\frac{1}{2}AB\)(2)
Từ (1) và (2) suy ra \(\frac{BK}{BC'}=\frac{BH}{AB}\)
Ta có: \(\widehat{KBH}=60^0-\widehat{ABK}=\widehat{ABC'}\)
\(\Delta KBH\)và \(\Delta C'BA\)có: \(\frac{BK}{BC'}=\frac{BH}{BA}\left(cmt\right)\); \(\widehat{KBH}=\widehat{C'BA}\left(cmt\right)\)
\(\Rightarrow\Delta KBH~\Delta C'BA\left(c-g-c\right)\)
\(\Rightarrow\frac{KH}{C'A}=\frac{1}{2}\Rightarrow\frac{KH}{AB'}=\frac{1}{2}\)và \(\widehat{C'AB}=\widehat{KHB}\)
Ta có: \(\widehat{HAB'}=\widehat{B'AC'}-\left(30^0+\widehat{C'AB}\right)\)
\(=\left(\widehat{B'AC'}-30^0\right)-\widehat{C'AB}=90^0-\widehat{KHB}=\widehat{KHA}\)
Mà \(\widehat{HAB'}\)và \(\widehat{KHA}\)ở vị trí so le trong nên KH // AB'
\(\Rightarrow\frac{KG}{GB'}=\frac{GH}{GA}=\frac{KH}{AB'}=\frac{1}{2}\)
hay \(\frac{B'G}{KB'}=\frac{GA}{HA}=\frac{2}{3}\)
Điều này chứng tỏ \(\Delta ABC\)và \(\Delta A'B'C'\)có cùng trọng tâm (đpcm)