Cho tỉ lệ thức \(\dfrac{ab}{a+b}=\dfrac{bc}{b+c}\). Chứng minh tỉ lệ thức: \(\dfrac{a}{b}=\dfrac{b}{c}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 10 2021
a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{5b}{5d}=\dfrac{3a}{4c}=\dfrac{4b}{4d}=\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\Rightarrow\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
14 tháng 10 2021
c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}\)
\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\dfrac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\dfrac{b^2}{d^2}\)
Do đó \(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
d, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\)
\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\)
Do đó \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
4 tháng 10 2023
Ta đặt:
\(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(a=b\times k\) ; \(c=d\times k\)
a) Ta có: \(\dfrac{a}{b}=\dfrac{b\times k}{d\times k}=\dfrac{b}{d}\) (1)
=> \(\dfrac{a+b}{c+d}=\dfrac{b\times k+b}{d\times k+d}=\dfrac{b\times\left(k+1\right)}{d\times\left(k+1\right)}=\dfrac{b}{d}\) (2)
Từ (1),(2) => đpcm
b)
\(\dfrac{a+b}{a}=\dfrac{b\times k+b}{b\times k}=\dfrac{b\times\left(k+1\right)}{b\times k}=\dfrac{k+1}{k}\) (1)
\(\dfrac{c+d}{c}=\dfrac{d\times k+d}{d\times k}=\dfrac{d\times\left(k+1\right)}{d\times k}=\dfrac{k+1}{k}\) (2)
Từ (1),(2) => đpcm
14 tháng 7 2021
\(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{a}{b}+1=\dfrac{c}{d}+1=>\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
\(\dfrac{a}{b}=\dfrac{c}{d}=>\dfrac{a}{b}-1=\dfrac{c}{d}-1=>\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
\(\dfrac{a}{b}=\dfrac{c}{d}=>ad=cb=>ad+ac=cb+ac\)
\(=>a\left(c+d\right)=c\left(a+b\right)=>\dfrac{a}{c}=\dfrac{a+b}{c+d}=>\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
5 tháng 1 2022
\(\Leftrightarrow\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}=\dfrac{a}{c}=\dfrac{b}{d}=>\dfrac{a}{b}=\dfrac{c}{d}\)
AH
Akai Haruma
Giáo viên
5 tháng 1 2022
Lời giải:
$\frac{a+b}{a-b}=\frac{c+d}{c-d}$
$\Rightarrow (a+b)(c-d)=(a-b)(c+d)$
$\Rightarrow ac-ad+bc-bd=ac+ad-bc-bd$
$\Rightarrow 2ad=2bc$
$\Rightarrow ad=bc$
$\Rightarrow \frac{a}{b}=\frac{c}{d}$ (đpcm)
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
a) Vì \(\dfrac{a}{b} = \dfrac{c}{d}\) nên \(ad = bc\)
Ta có \(\dfrac{{a + b}}{b} = \dfrac{{c + d}}{d}\)\( \Rightarrow d(a + b) = b(c + d)\)\( \Rightarrow ad + bd = bc + bd\)
\( \Rightarrow ad = bc\) (luôn đúng)
\( \Rightarrow \dfrac{{a + b}}{b} = \dfrac{{c + d}}{d}\)
b) Vì \(\dfrac{a}{b} = \dfrac{c}{d}\) nên \(ad = bc\)
Ta có: \(\dfrac{{a - b}}{b} = \dfrac{{c - d}}{d}\)
\(\begin{array}{l} \Rightarrow d(a - b) = b(c - d)\\ \Leftrightarrow ad - bd = bc - bd\\ \Leftrightarrow ad = bc\end{array}\) ( luôn đúng)
Vậy \(\dfrac{{a - b}}{b} = \dfrac{{c - d}}{d}\)
c) Vì \(\dfrac{a}{b} = \dfrac{c}{d}\) nên \(ad = bc\)
Ta có: \(\dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
\(\begin{array}{l} \Rightarrow a(c + d) = c(a + b)\\ \Leftrightarrow ac + ad = ac + bc\\ \Leftrightarrow ad = bc\end{array}\) (luôn đúng)
Vậy \(\dfrac{a}{{a + b}} = \dfrac{c}{{c + d}}\)
23 tháng 9 2017
a/ Đặt :
\(\dfrac{a}{b}=\dfrac{c}{d}=k\)\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có :
\(VT=\dfrac{a-b}{a+b}=\dfrac{bk-b}{bk+b}=\dfrac{b\left(k-1\right)}{b\left(k+1\right)}=\dfrac{k-1}{k+1}\)\(\left(1\right)\)
\(VP=\dfrac{c-d}{c+d}=\dfrac{dk-d}{dk+d}=\dfrac{d\left(k-1\right)}{d\left(k+1\right)}=\dfrac{k-1}{k+1}\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrowđpcm\)
b/ Đặt :
\(\dfrac{a}{b}=\dfrac{c}{d}=k\)\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
\(VT=\dfrac{2a+5b}{3a-4b}=\dfrac{2bk+5b}{3bk-4b}=\dfrac{b\left(2k+5\right)}{b\left(3k-4\right)}=\dfrac{2k+5}{3k-4}\left(1\right)\)
\(VP=\dfrac{2c+5d}{3c-4d}=\dfrac{2dk+5d}{3dk-4d}=\dfrac{d\left(2k+5\right)}{d\left(3k-4\right)}=\dfrac{2k+5}{3k-4}\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrowđpcm\)
28 tháng 9 2018
a) Từ \(\dfrac{a}{b}=\dfrac{c}{d}\) \(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\)
Từ \(\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\) \(\Rightarrow\dfrac{c-d}{c+d}=\dfrac{a-b}{a+b}\)
b) Từ \(\dfrac{a}{b}=\dfrac{c}{d}\) \(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{3a}{3c}=\dfrac{4b}{4d}=\dfrac{5b}{5d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{2a}{2c}=\dfrac{3a}{3c}=\dfrac{4b}{4d}=\dfrac{5b}{5d}=\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\)
Từ \(\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\) \(\Rightarrow\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
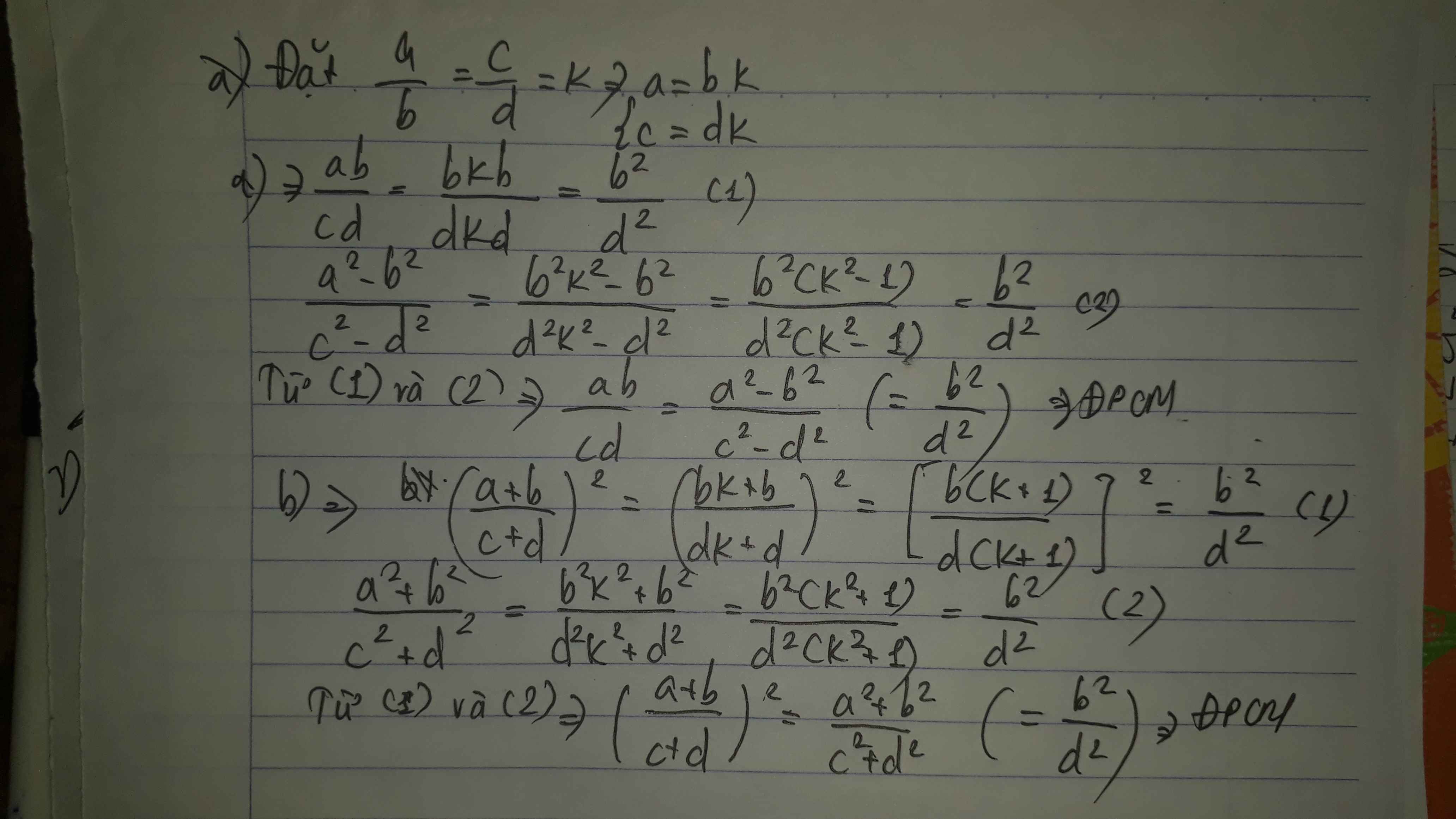
\(\dfrac{ab}{a+b}=\dfrac{bc}{b+c}\)
\(\Rightarrow ab\left(b+c\right)=bc\left(a+b\right)\)
\(\Rightarrow ab^2+abc=abc+b^2c\)
\(\Rightarrow ab^2=b^2c\)
\(\Rightarrow a=c\)
Đến đây ko còn manh mối :v