a, \(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2015}{2017}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 + \(\dfrac{1}{3}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{10}\) + ... + \(\dfrac{2}{x\left(x+1\right)}\) = 1\(\dfrac{2015}{2017}\)
=> \(\dfrac{2}{2}\) + \(\dfrac{2}{6}\) + \(\dfrac{2}{12}\) + \(\dfrac{2}{20}\) + ... + \(\dfrac{2}{x\left(x+1\right)}\) = 1\(\dfrac{2015}{2017}\)
=> \(\dfrac{2}{1.2}\) + \(\dfrac{2}{2.3}\) + \(\dfrac{2}{3.4}\) + \(\dfrac{2}{4.5}\) + ... + \(\dfrac{2}{x\left(x+1\right)}\) = 1\(\dfrac{2015}{2017}\)
=> \(\dfrac{1.2}{1.2}\) + \(\dfrac{1.2}{2.3}\) + \(\dfrac{1.2}{3.4}\) + \(\dfrac{1.2}{4.5}\) + ... + \(\dfrac{1.2}{x\left(x+1\right)}\) = 1\(\dfrac{2015}{2017}\)
=> 2(\(\dfrac{1}{1.2}\)+ \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\) + ... + \(\dfrac{1}{x\left(x+1\right)}\)) = 1\(\dfrac{2015}{2017}\)
=> 2(1 - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + ... + \(\dfrac{1}{x}\) - \(\dfrac{1}{x+1}\)) = 1\(\dfrac{2015}{2017}\)
=> 2(1 - \(\dfrac{1}{x+1}\)) = \(\dfrac{4032}{2017}\)
=> 1 - \(\dfrac{1}{x+1}\) = \(\dfrac{4032}{2017}\) : 2
=> 1 - \(\dfrac{1}{x+1}\) = \(\dfrac{2016}{2017}\)
=> \(\dfrac{1}{x+1}\) = 1 - \(\dfrac{2016}{2017}\)
=> \(\dfrac{1}{x+1}\) = \(\dfrac{1}{2017}\)
=> x + 1 = 2017
=> x = 2017 - 1
=> x = 2016

Sửa đề:\(\dfrac{1}{3}+\dfrac{1}{6}+\dfrac{1}{10}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2015}{2017}\)
\(\Leftrightarrow\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{20}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2015}{2017}\)
\(\Leftrightarrow\dfrac{2}{2.3}+\dfrac{2}{3.4}+\dfrac{2}{4.5}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2015}{2017}\)
\(\Leftrightarrow1-\dfrac{2}{3}+\dfrac{2}{3}-\dfrac{2}{4}+\dfrac{2}{4}-\dfrac{2}{5}+...+\dfrac{2}{x}-\dfrac{2}{x+1}=\dfrac{2015}{2017}\)
\(\Leftrightarrow1-\dfrac{2}{x+1}=\dfrac{2015}{2017}\Leftrightarrow\dfrac{2}{x+1}=1-\dfrac{2015}{2017}=\dfrac{2}{2017}\)
Do \(\dfrac{2}{x+1}=\dfrac{2}{2017}\Rightarrow x+1=2017\Leftrightarrow x=2016\)

Lời giải:
Ta thấy: \(f(x)=\frac{x^3}{1-3x+3x^2}\Rightarrow f(1-x)=\frac{(1-x)^3}{1-3(1-x)+3(1-x)^2}=\frac{(1-x)^3}{3x^2-3x+1}\)
\(\Rightarrow f(x)+f(1-x)=\frac{x^3}{1-3x+3x^2}+\frac{(1-x)^3}{3x^2-3x+1}=\frac{x^3+(1-x)^3}{3x^2-3x+1}=1\)
Do đó:
\(f\left(\frac{1}{2017}\right)+f\left(\frac{2016}{2017}\right)=1\)
\(f\left(\frac{2}{2017}\right)+f\left(\frac{2015}{2017}\right)=1\)
............
\(f\left(\frac{1008}{2017}\right)+f\left(\frac{1009}{2017}\right)=1\)
Cộng theo vế:
\(\Rightarrow A=f\left(\frac{1}{2017}\right)+f\left(\frac{2}{2017}\right)+f\left(\frac{3}{2017}\right)+...f\left(\frac{2015}{2017}\right)+f\left(\frac{2016}{2017}\right)\)
\(=\underbrace{1+1+1...+1}_{1008}=1008\)

\(A=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\left(\dfrac{1}{4}-1\right)...\left(\dfrac{1}{2015}-1\right)\left(\dfrac{1}{2016}-1\right)\left(\dfrac{1}{2017}-1\right)\\ A=\left(-\dfrac{1}{2}\right).\left(-\dfrac{2}{3}\right).\left(-\dfrac{3}{4}\right)...\left(-\dfrac{2014}{2015}\right)\left(-\dfrac{2015}{2016}\right)\left(-\dfrac{2016}{2017}\right)\\ A=\dfrac{1.2.3.4...2014.2015.2016}{2.3.4...2015.2016.2017}=\dfrac{1}{2017}\)
\(B=\left(-1\dfrac{1}{2}\right)\left(-1\dfrac{1}{3}\right)\left(-1\dfrac{1}{4}\right)...\left(-1\dfrac{1}{2015}\right)\left(-1\dfrac{1}{2016}\right)\left(-1\dfrac{1}{2017}\right)\\ B=\left(-\dfrac{3}{2}\right)\left(-\dfrac{4}{3}\right)\left(-\dfrac{5}{4}\right)...\left(-\dfrac{2016}{2015}\right)\left(-\dfrac{2017}{2016}\right)\left(-\dfrac{2018}{2017}\right)\\ B=\dfrac{3.4.5...2016.2017.2018}{2.3.4...2015.2016.2017}=\dfrac{2018}{2}=1009\)
\(M=A.B=\dfrac{1}{2017}.1009=\dfrac{1009}{2017}\)

a) Vì \(\dfrac{x+5}{3}\)= \(\dfrac{x-6}{7}\) nên 7(x+5) = 3(x-6)
=> 7x+ 35 = 3x - 18
7x - 3x = -18 -35
4x = -53
x = -53:4
x = \(\dfrac{-53}{4}\)

a: \(\Leftrightarrow\dfrac{7}{2}x-\dfrac{3}{4}=\dfrac{1}{2}x+\dfrac{5}{2}\)
\(\Leftrightarrow3x=\dfrac{5}{2}+\dfrac{3}{4}=\dfrac{10}{4}+\dfrac{3}{4}=\dfrac{13}{4}\)
=>x=13/12
b: \(\Leftrightarrow x\cdot\left(\dfrac{2}{3}-\dfrac{1}{2}\right)=-\dfrac{1}{3}+\dfrac{2}{5}\)
\(\Leftrightarrow x\cdot\dfrac{1}{6}=\dfrac{-5+6}{15}=\dfrac{1}{15}\)
\(\Leftrightarrow x=\dfrac{1}{15}:\dfrac{1}{6}=\dfrac{2}{5}\)
c: \(\Leftrightarrow x\cdot\dfrac{1}{3}+x\cdot\dfrac{2}{5}+\dfrac{2}{5}=0\)
\(\Leftrightarrow x\cdot\dfrac{11}{15}=-\dfrac{2}{5}\)
\(\Leftrightarrow x=-\dfrac{2}{5}:\dfrac{11}{15}=\dfrac{-2}{5}\cdot\dfrac{15}{11}=\dfrac{-30}{55}=\dfrac{-6}{11}\)
d: \(\Leftrightarrow-\dfrac{1}{3}x+\dfrac{1}{2}+\dfrac{2}{3}-x-\dfrac{1}{2}=5\)
\(\Leftrightarrow-\dfrac{4}{3}x+\dfrac{2}{3}=5\)
\(\Leftrightarrow-\dfrac{4}{3}x=5-\dfrac{2}{3}=\dfrac{13}{3}\)
\(\Leftrightarrow x=\dfrac{13}{3}:\dfrac{-4}{3}=\dfrac{-13}{4}\)
e: \(\Leftrightarrow\left(\dfrac{x+2015}{5}+1\right)+\left(\dfrac{x+2016}{4}+1\right)=\left(\dfrac{x+2017}{3}+1\right)+\left(\dfrac{x+2018}{2}+1\right)\)
=>x+2020=0
hay x=-2020

\(\dfrac{1}{3}+\dfrac{1}{6}+....+\dfrac{2}{x\left(x+1\right)}=\dfrac{2017}{2019}\\ \Rightarrow\dfrac{2}{6}+\dfrac{2}{12}+...+\dfrac{2}{x\left(x+1\right)}=\dfrac{2017}{2019}\\ \Rightarrow2.\left(\dfrac{1}{2}-\dfrac{1}{x+1}\right)=\dfrac{2017}{2019}\\ \Rightarrow\dfrac{1}{2}-\dfrac{1}{x+1}=\dfrac{2017}{4038}\\ \Rightarrow\dfrac{1}{x+1}=\dfrac{1}{2019}\\ \Rightarrow x=2018\)

ĐKXĐ: \(x\ge0,x\ne1\)
\(A=\left(1+\dfrac{\sqrt{x}}{x+1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right)-1\)
= \(\dfrac{x+\sqrt{x}+1}{x+1}:\left(\dfrac{x+1-2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\right)-1\)
= \(\dfrac{\left(x+\sqrt{x}+1\right)\left(x+1\right)\left(\sqrt{x}-1\right)}{\left(x+1\right)\left(\sqrt{x}-1\right)^2}-1\)
= \(\dfrac{x+\sqrt{x}+1}{\sqrt{x}-1}-1\)
= \(\dfrac{x+\sqrt{x}+1-\sqrt{x}+1}{\sqrt{x}-1}\)
= \(\dfrac{x+2}{\sqrt{x}-1}\)
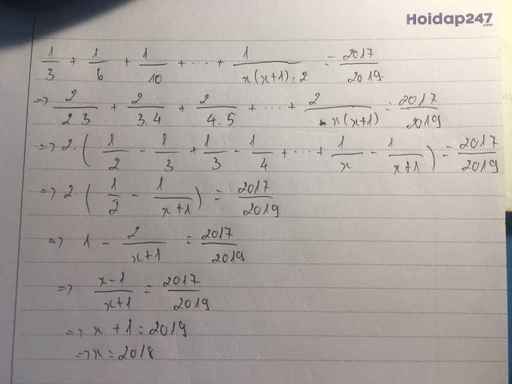
\(\Leftrightarrow2\left(\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{x\left(x+1\right)}\right)=\dfrac{2015}{2017}\)
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{2015}{4034}\)
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{x+1}=\dfrac{2015}{4034}\)
\(\Leftrightarrow\dfrac{1}{x+1}=\dfrac{1}{2017}\)
=>x+1=2017
hay x=2016