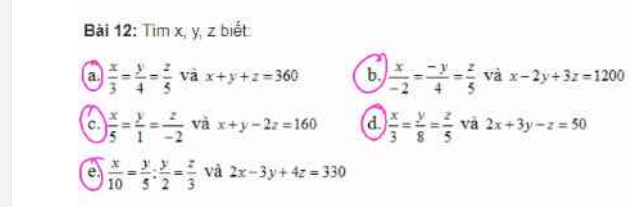giải giúp mình bài này cảm ơn trước
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TV
3
7 tháng 12 2021
\(9,PT\Leftrightarrow x-6=3x-7\left(x\ge6\right)\\ \Leftrightarrow x=\dfrac{1}{2}\left(ktm\right)\\ \Leftrightarrow x\in\varnothing\\ 10,PT\Leftrightarrow3x-2=4x^2-4x+1\left(x\le\dfrac{1}{2}\right)\\ \Leftrightarrow4x^2-7x+3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{4}\end{matrix}\right.\left(ktm\right)\Leftrightarrow x\in\varnothing\\ 11,PT\Leftrightarrow\sqrt{x^2+x-1}=2-x\left(x\le2\right)\\ \Leftrightarrow x^2+x-1=x^2-4x+4\\ \Leftrightarrow5x=5\Leftrightarrow x=1\left(tm\right)\\ 12,PT\Leftrightarrow\left(\sqrt{20-x}-4\right)+\left(\sqrt{x+5}-3\right)=0\left(5\le x\le20\right)\\ \Leftrightarrow\dfrac{4-x}{\sqrt{20-x}+4}+\dfrac{x-4}{\sqrt{x+5}+3}=0\\ \Leftrightarrow\left(x-4\right)\left(\dfrac{1}{\sqrt{x+5}+3}-\dfrac{1}{\sqrt{20-x}+4}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\\dfrac{1}{\sqrt{x+5}+3}=\dfrac{1}{\sqrt{20-x}+4}\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\sqrt{x+5}+3=\sqrt{20-x}+4\\ \Leftrightarrow\left(\sqrt{x+5}-4\right)-\left(\sqrt{20-x}-3\right)=0\\ \Leftrightarrow\dfrac{x-11}{\sqrt{x+5}+4}+\dfrac{x-11}{\sqrt{20-x}+3}=0\\ \Leftrightarrow\left(x-11\right)\left(\dfrac{1}{\sqrt{x+5}+4}+\dfrac{1}{\sqrt{20-x}+3}\right)=0\\ \Leftrightarrow x=11\left(\dfrac{1}{\sqrt{x+5}+4}+\dfrac{1}{\sqrt{20-x}+3}>0\right)\\ \text{Vậy PT có nghiệm }x\in\left\{4;11\right\}\)
7 tháng 12 2021
\(13,PT\Leftrightarrow\sqrt{x-1}+\sqrt{3x-2}=\sqrt{5x+1}\left(x\ge-\dfrac{1}{5}\right)\\ \Leftrightarrow4x-3+2\sqrt{\left(x-1\right)\left(3x-2\right)}=5x+1\\ \Leftrightarrow x+4=2\sqrt{3x^2-5x+2}\\ \Leftrightarrow x^2+8x+16=12x^2-20x+8\\ \Leftrightarrow11x^2-28x-8=0\\ \Delta'=14^2+8\cdot11=284\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{14-2\sqrt{71}}{11}\\x=\dfrac{14+2\sqrt{71}}{11}\end{matrix}\right.\)
\(14,ĐK:x\ge-1\)
Đặt \(\sqrt{x+1}=a\ge0\)
\(PT\Leftrightarrow2\sqrt{a^2-1+2a}-a=4\\ \Leftrightarrow2\sqrt{a^2+2a-1}=a+4\\ \Leftrightarrow4a^2+8a-4=a^2+8a+16\\ \Leftrightarrow3a^2-20=0\\ \Leftrightarrow a^2=\dfrac{20}{3}\Leftrightarrow x+1=\dfrac{20}{3}\Leftrightarrow x=\dfrac{17}{3}\left(tm\right)\)
\(15,ĐK:-3\le x\le6\)
Đặt \(\sqrt{x+3}+\sqrt{6-x}=a\ge0\)
\(\Leftrightarrow\dfrac{a^2-9}{2}=\sqrt{\left(x+3\right)\left(6-x\right)}\\ PT\Leftrightarrow a-\dfrac{a^2-9}{2}=3\\ \Leftrightarrow2a-a^2+9=6\\ \Leftrightarrow a^2-2a-3=0\\ \Leftrightarrow a=3\left(a\ge0\right)\\ \Leftrightarrow\sqrt{x+3}+\sqrt{6-x}=3\\ \Leftrightarrow\sqrt{x+3}-3+\sqrt{6-x}=0\\ \Leftrightarrow\dfrac{x-6}{\sqrt{x+3}+3}-\dfrac{x-6}{\sqrt{6-x}}=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\left(tm\right)\\\dfrac{1}{\sqrt{x+3}+3}=\dfrac{1}{\sqrt{6-x}}\left(1\right)\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\sqrt{x+3}+3=\sqrt{6-x}\\ \Leftrightarrow\sqrt{x+3}-\left(\sqrt{6-x}-3\right)=0\\ \Leftrightarrow\dfrac{x+3}{\sqrt{x+3}}+\dfrac{x+3}{\sqrt{6-x}+3}=0\\ \Leftrightarrow x=-3\left(\dfrac{1}{\sqrt{x+3}}+\dfrac{1}{\sqrt{6-x}+3}>0\right)\\ \text{Vậy PT có nghiệm }x\in\left\{6;-3\right\}\)
NT
9
4 tháng 3 2022
\(\dfrac{4}{7}+\dfrac{2}{9}+\dfrac{1}{4}+\dfrac{3}{7}+\dfrac{7}{9}+\dfrac{75}{100}\\ =\dfrac{4}{7}+\dfrac{2}{9}+\dfrac{1}{4}+\dfrac{3}{7}+\dfrac{7}{9}+\dfrac{3}{4}\\ =\left(\dfrac{4}{7}+\dfrac{3}{7}\right)+\left(\dfrac{2}{9}+\dfrac{7}{9}\right)+\left(\dfrac{1}{4}+\dfrac{3}{4}\right)\\ =\dfrac{7}{7}+\dfrac{9}{9}+\dfrac{4}{4}\\ =1+1+1\\ =3\)
Ta có: \(\dfrac{7}{11}=\dfrac{7\times3}{11\times3}=\dfrac{21}{33};\dfrac{8}{11}=\dfrac{8\times3}{11\times3}=\dfrac{24}{33}\)
2 phân số giữa là: \(\dfrac{22}{33};\dfrac{23}{33}\)
4 tháng 3 2022
\(=\left(\dfrac{4}{7}+\dfrac{3}{7}\right)+\left(\dfrac{2}{9}+\dfrac{7}{9}\right)+\left(\dfrac{1}{4}+\dfrac{3}{4}\right)=1+1+1=3\)
NT
0
ST
0
1 tháng 11 2021
a: \(=2\sqrt{2}\cdot\sqrt{2}-3\sqrt{2}\cdot\sqrt{2}+\sqrt{10}\cdot\sqrt{2}-2\sqrt{5}\)
=4-6
=-2
b: \(=8+2\sqrt{15}-8+2\sqrt{15}=4\sqrt{15}\)
a) Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y+z}{3+4+5}=\dfrac{360}{60}=6\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=6\\\dfrac{y}{4}=6\\\dfrac{z}{5}=6\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=18\\y=24\\z=30\end{matrix}\right.\)
b) Áp dụng tính chất dãy tỉ số bằng nhau:\(\dfrac{x}{-2}=-\dfrac{y}{4}=\dfrac{z}{5}=-\dfrac{2y}{8}=\dfrac{3z}{15}=\dfrac{x-2y+3z}{-2+8+15}=\dfrac{1200}{21}=\dfrac{400}{7}\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{-2}=\dfrac{400}{7}\\-\dfrac{y}{4}=\dfrac{400}{7}\\\dfrac{z}{5}=\dfrac{400}{7}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{800}{7}\\y=-\dfrac{1600}{7}\\z=\dfrac{2000}{7}\end{matrix}\right.\)
c) Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{x}{5}=\dfrac{y}{1}=\dfrac{z}{-2}=\dfrac{-2z}{4}=\dfrac{x+y-2z}{5+1+4}=\dfrac{160}{10}=16\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=16\\\dfrac{y}{1}=16\\\dfrac{z}{-2}=16\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=80\\y=16\\z=-32\end{matrix}\right.\)
Cảm ơn bạn nha