Cho tam giác ABC vuông tại A, đường cao AH. Gọi HE, HF lần lượt là các đường cao của tam giác AHB, AHC.
a)chứng tỏ:BC2 = 3AH2+BE2+CF2
b)giả sử BC=2a là độ dài cố định. Tìm giá trị nhỏ nhất của BE2+CF2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
30 tháng 7 2017
Hình thì e tự vẽ nha
a) Dễ dàng c/m đc AEHF là hcn => AH = EF
Áp dụng hệ thức lượng ta có
\(BC^2=\left(BH+CH\right)^2=BH^2+CH^2+2AH.BH\)
\(=BE^2+HE^2+CF^2+HF^2+2AH^2=BE^2+CF^2+2AH^2+\left(HE^2+HF^2\right)\)
\(=BE^2+CF^2+2AH^2+EF^2=BE^2+CF^2+2AH^2+AH^2\)
\(=BE^2+CF^2+3AH^2\)
b) \(\Delta ABH\) có \(BE=\frac{BH^2}{AB}\) \(\Rightarrow BE^2=\frac{BH^4}{AB^2}\)
Tương tự \(CF^2=\frac{CH^4}{AC^2}\)
Áp dụng BĐT Cauchy-Schwarz dạng Engel và BĐT \(a^2+b^2\ge\frac{\left(a+b\right)^2}{2}\)
Do đó \(BE^2+CF^2=\frac{BH^4}{AB^2}+\frac{CH^4}{AC^2}\ge\frac{\left(BH^2+CH^2\right)^2}{AB^2+AC^2}\ge\frac{\left[\frac{\left(BH+CH\right)^2}{2}\right]^2}{BC^2}=\frac{\left[\frac{BC^2}{2}\right]^2}{BC^2}\)
\(=\frac{\frac{BC^4}{4}}{BC^2}=\frac{BC^2}{4}=\frac{\left(2a\right)^2}{4}=a^2\)
Đẳng thức xảy ra \(\Leftrightarrow BH=CH\) hay H là trung điểm BC.
Như vậy AH vừa là đường cao, vừa là đường trung tuyến
=> Tam giác ABC vuông cân tại A.
p/s: làm lụi thôi nha, ko bt đúng ko nữa. Đúng thì cho mk 1 k nha
16 tháng 6 2015
a, áp dụng hệ thức lượng cho các tam giác vuông AHB,AHC, ABC có các đường cao ta có:\(BE=\frac{BH^2}{AB};CF=\frac{HC^2}{AC};BE.CF=\frac{BH^2.HC^2}{AB.AC}=\frac{AH^4}{AB.AC}\); \(BC=\frac{AB^2}{AH}\)
\(BC.CE.CF=\frac{AB^2}{AH}.\frac{AH^4}{AB.AC}=\frac{AH^3.AB}{AC}=AH^3.\frac{AB}{AC}\).
tam giác này người ta k cho cân => AB/AC không =1 đc => BC.BE.CF khác AH^3
\(EB=\frac{BH^2}{AB};FC=\frac{HC^2}{AC}\Rightarrow\frac{EB}{FC}=\frac{BH^2.AC}{AB.HC^2}\). VỚI TAM GIÁC ABC TA CÓ: \(BH=\frac{AB^2}{BC}\Rightarrow BH^2=\frac{AB^4}{BC}\Leftrightarrow HC^2=\frac{AC^4}{BC}\) => \(\frac{EB}{FC}=\frac{\frac{AB^4}{BC}.AC}{AB.\frac{AC^4}{BC}}=\frac{AB^4.AC.BC}{AB.AC^4.BC}=\frac{AB^3}{AC^3}\)
B) C/M TỨ GIÁC AEHF LÀ HÌNH CHỮ NHẬT => EF=AH(T/C) => EF LỚN NHẤT <=> AH LỚN NHẤT
TỪ A KẺ TRUNG TUYẾN AM. \(AH\le AM\) (ĐƯỜNG VUÔNG GÓC VÀ ĐƯỜNG XIÊN) => AH LỚN NHẤT KHI AH=AM <=> AH=1/2 BC=1/2a<=> EF LỚN NHẤT =1/2a (AM LÀ TRUNG TUYẾN CỦA TAM GIÁC VUÔNG => = 1/2 CẠNH HUYỀN)
TỪ CÁC CÔNG THỨC ĐÃ LẬP Ở TRÊN, S AEHF=AE.AF=\(\frac{AH^2}{AB}.\frac{AH^2}{AC}=\frac{AH^4}{AB.AC}=\frac{AH^4}{\sqrt{BH.BC.HC.BC}}=\frac{AH^4}{BC\sqrt{AH^2}}=\frac{AH^3}{BC}\)
CHỈ LÀM ĐC ĐẾN ĐÂY THÔI :-/ DÙ SAO CŨNG ĐC ÍT NHIỀU :)
AT
16 tháng 7 2021
a) đề phải là \(\dfrac{EB}{FC}=\dfrac{AB^3}{AC^3}\)
Ta có: \(\dfrac{EB}{FC}.\dfrac{AB}{AC}=\dfrac{BE.BA}{AC.CF}=\dfrac{BH^2}{CH^2}=\left(\dfrac{BH}{CH}\right)^2=\left(\dfrac{BH.BC}{CH.BC}\right)^2\)
\(=\left(\dfrac{AB^2}{AC^2}\right)^2=\dfrac{AB^4}{AC^4}\Rightarrow\dfrac{EB}{FC}=\dfrac{AB^3}{AC^3}\)
b) Vì \(\angle HEA=\angle HFA=\angle EAF=90\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow AH^2=EF^2=EH^2+HF^2\)
Ta có: \(3AH^2+BE^2+CF^2=\left(BE^2+EH^2\right)+\left(CF^2+FH^2\right)+2AH^2\)
\(=BH^2+CH^2+2.BH.CH=\left(BH+CH\right)^2=BC^2\)
23 tháng 6 2017
a, bc^2 = ab^2 +ac^2
<=.> (ae+eb)^2 +(af+fc)^2
<=.>AE^2 +2 AE.EB +EB^2 +AF^2+FC^2+2AF,FC
<=> EF^2 +EB^2 +CF^2 +2.(EH^2+FH^2)
<=>EB^2 +CF^2 + AH ^2 + 2 AH^2 vì tứ giác EHAF là hcn suy ra AH =EF
<=>EB^2 +CF^2+3 AH^2 (đpcm)
b, cb =2a là thế nào vậy
3 tháng 7 2021
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{HB}{HC}\)(đpcm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB, ta được:
\(BD\cdot BA=BH^2\)
\(\Leftrightarrow BD=\dfrac{HB^2}{AB}\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(CE\cdot CA=CH^2\)
\(\Leftrightarrow EC=\dfrac{HC^2}{AC}\)
Ta có: \(\dfrac{BD}{EC}=\dfrac{HB^2}{AB}:\dfrac{HC^2}{AC}\)
\(\Leftrightarrow\dfrac{BD}{EC}=\dfrac{HB^2}{AB}\cdot\dfrac{AC}{HC^2}\)
\(\Leftrightarrow\dfrac{BD}{EC}=\left(\dfrac{HB}{HC}\right)^2\cdot\dfrac{AC}{AB}\)
\(\Leftrightarrow\dfrac{BD}{EC}=\left(\dfrac{AB}{AC}\right)^4\cdot\dfrac{AC}{AB}=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)(đpcm)
2 tháng 8 2019
Câu hỏi của Nguyễn Tấn Phát - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo!
Bạn tự vẽ hình nha!
a) CMR :
và 
nên tứ giác EHFA là hình chữ nhật .
^2+(FA+FC)^2=(BE^2+CF^2)+EA^2+AF^2+2.EB.EA+2.FA.FC)
)
)
=2(EH^2+EA^2)=2.AH^2)
biết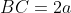 
.
=BH^2+CH^2-(EH^2+EA^2))
(do 
)
(theo Cosi)
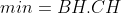. Dấu "=" khi 
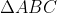vuông cân ở A .
.
Tứ giác EHFA có
Ta có :
Vậy , ta phải CMR :
Xét tam giác vuông BHA :
Xét tam giác vuông CHA :
Cộng (1) với (2) :
Mà
Suy ra điều phải chứng minh .
b) Tìm min của
Cộng lại :
=>
<=>
a) auto prove
b) Ta có:\(BE.AB=BH^2\)(hệ thức về cạnh và đường cao trong tg v)
\(\Rightarrow BE=\dfrac{BH^2}{AB}\)\(\Rightarrow BE^2=\dfrac{BH^4}{AB^2}\)
Tương tự với CF,ta có: \(BE^2+CF^2=\dfrac{BH^4}{AB^2}+\dfrac{HC^4}{AC^2}\ge\dfrac{\left(HB^2+HC^2\right)^2}{AB^2+AC^2}\)( BĐT cauchy-schwarz)
Mà \(HB^2+HC^2\ge\dfrac{1}{2}\left(HB+HC\right)^2=\dfrac{1}{2}.BC^2\)(BĐT bunyakovsky)
\(\Rightarrow BE^2+CF^2\ge\dfrac{\dfrac{1}{4}BC^4}{BC^2}=\dfrac{BC^2}{4}=\dfrac{4a^2}{4}=a^2\)
Dấu = xảy ra khi tam giác ABC vuông cân ở A