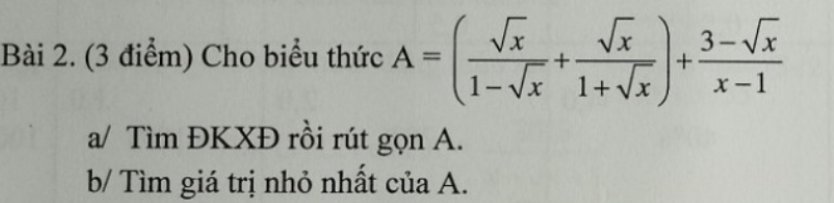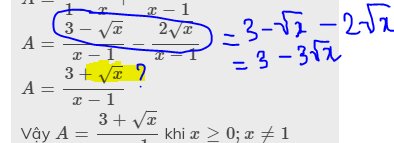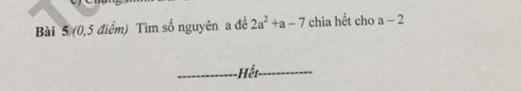Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) \(\dfrac{x}{2}=\dfrac{-18}{5}\)
\(\Rightarrow x=\dfrac{\left(-18\right).2}{5}=-\dfrac{36}{5}\)
b) \(x:\left(-\dfrac{1}{2}\right)=\dfrac{5}{8}\)
\(\Rightarrow x=\dfrac{5}{8}.\left(-\dfrac{1}{2}\right)=-\dfrac{5}{16}\)

1: Xét (O) có
ΔABD nội tiếp
AB là đường kính
Do đó: ΔABD vuông tại D
=>AD\(\perp\)BD tại D
=>BD\(\perp\)AC tại D
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE\(\perp\)EB tại E
=>AE\(\perp\)CB tại E
Xét ΔCAB có
AE,BD là các đường cao
AE cắt BD tại H
Do đó: H là trực tâm của ΔCAB
=>CH\(\perp\)AB tại K
2: ΔCDH vuông tại D
mà DF là đường trung tuyến
nên DF=FH
=>ΔFDH cân tại F
=>\(\widehat{FDH}=\widehat{FHD}\)
mà \(\widehat{FHD}=\widehat{KHB}\)(hai góc đối đỉnh)
và \(\widehat{KHB}=\widehat{DAB}\left(=90^0-\widehat{DBA}\right)\)
nên \(\widehat{FDH}=\widehat{DAB}\)
Ta có: ΔOBD cân tại O
=>\(\widehat{ODB}=\widehat{OBD}=\widehat{DBA}\)
\(\widehat{FDO}=\widehat{FDH}+\widehat{ODB}\)
\(=\widehat{DBA}+\widehat{DAB}=90^0\)
=>DF là tiếp tuyến của (O)

`a,` ĐKXĐ: `x>=0;x\ne1`
`A=...=(sqrtx(1+sqrtx)+sqrtx(1-sqrtx)+sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=(sqrtx+x+sqrtx-x+sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=(3sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=-3/(1+sqrtx)`
`b,A=-3/(1+sqrtx)`
Vì `x>=0` nên `1+sqrtx>=1` nên `3/(1+sqrtx)<=3` suy ra `A>=-3`
Dấu "=" xảy ra `<=>x=0`
Vậy `A_(min)=-3<=>x=0`

reffer
- Theo em, tầng lớp hào trưởng bản địa hình thành từ bộ phận quý tộc trong xã hội Âu Lạc cũ sẽ là thủ lĩnh của những cuộc đấu tranh giành độc lập của người Việt. Vì: các hào trưởng là những người có uy tín và vị thế quan trọng trong xã hội do đó, họ sẽ dễ dàng huy động, liên kết các tầng lớp nhân dân khác tham gia vào cuộc đấu tranh chống ngoại xâm.

Thực hiện phép chia:
(2a^2+a-7):(x-2) được dư là 3
Để 2a^2+a-7 chia hết cho a-2
thì 3 chia hết cho a-2
=>a-2€Ư(3)
=>a-2=1<=>a=3(nhận)
a-2=-1<=>a=1(nhận)
a-2=3<=>a=5(nhận)
a-2=-3<=>a=-1(nhận)
Vây, a€{3;1;5;-1} để (2a^2+a-7)chia hết cho (a-2) l

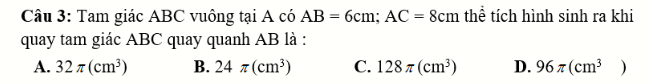

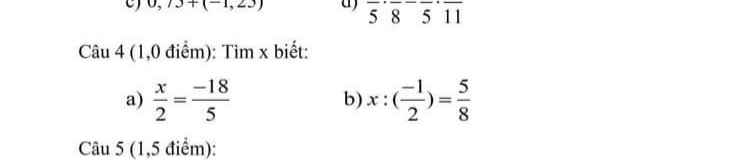

 Giải giúp mik câu này ạ ngày may mik thi r 🥺
Giải giúp mik câu này ạ ngày may mik thi r 🥺