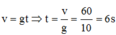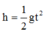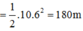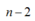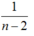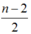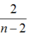Tại cùng một vị trí có độ cao h so với mặt đất, người ta lần lượt thả hai vật rơi tự do không vận tốc đầu. Sau 2s kể từ lúc vật thứ hai bắt đầu rơi, khoảng cách giữa hai vật là 25m. Tính xem vật thứ hai rơi sau vật thứ nhất bao lâu ? Cho g=10m/s2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+)Gọi thời gian vật 2 rơi sau vật 1 là t (s)
+) Ta có phương trình khoảng cách của 2s kể từ lúc vật 2 rơi so với vật 1:
Svật1 - Svật2 = 2,5
<=> \(\dfrac{\left(t+2\right)^2}{2}.10\) - \(\dfrac{2^2}{2}.10\) = 2,5
=> t=0,12132 (s)

a) Theo bài ra, ta có:
v2 - vo2 =2.g.h
⇒ \(h=\dfrac{v^2}{2g}=45\left(m\right)\)
b) Quãng đường vật rơi trong 2s đầu là:
\(h'=\dfrac{1}{2}gt^2=\dfrac{1}{2}.10.2^2=20\left(m\right)\)
Quãng đường vật rơi trong giây thứ 2 chính bằng quãng đường đi trong 2s đầu quãng đường đi trong 1s đầu
\(20-\dfrac{1}{2}.10.1^2=15\left(m\right)\)

Đáp án D
Chọn trục Ox thẳng đứng, gốc O tại mặt đất, chiều dương hướng lên
Thời gian vật rơi được khoảng h/n là : 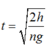 (1)
(1)
Tại điểm hai vật gặp nhau, với vật ném lên ta có :
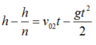 (2)
(2)
(1) và (2)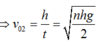
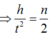
Mà ![]()
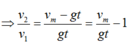
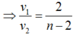

a , Theo bài ra ta có v2 - vo2 =2.g.h
=> h=\(\frac{v^2}{2g}=45\left(m\right)\)
Vậy độ cao ......
b , - Quãng đường vật rơi trong 2s đầu là
h' = \(\frac{1}{2}gt^2=\frac{1}{2}.10.2^2=20\left(m\right)\)
- Quãng đường vật rơi trong giây thứ 2 chính bằng quãng đường đi trong 2s đầu - quãng đường đi trong 1s đầu
20 - \(\frac{1}{2}.10.1^2\) = 15 ( m)
Vậy .....................................

`@W_t=mgz=2.10.2=40(J)`
`W_đ=1/2mv^2=1/2 .2.0^2=0(J)`
`W=W_t+W_đ=40+0=40(J)`
`@W_[(W_đ=2W_t)]=W_[đ(W_đ=2W_t)]+W_[t(W_đ=2W_t)]=40`
Mà `W_[đ(W_đ=2W_t)]=2W_[t(W_đ=2W_t)]`
`=>3W_[t(W_đ=2W_t)]=40`
`<=>3mgz_[(W_đ=2W_t)]=40`
`<=>3.2.10.z_[(W_đ=2W_t)]=40`
`<=>z_[(W_đ=2W_t)]~~0,67(m)`
`@W_[đ(max)]=W_[t(max)]=40`
`<=>1/2mv_[max] ^2=40`
`<=>1/2 .2v_[max] ^2=40`
`<=>v_[max]=2\sqrt{10}(m//s)`
Sao lại 3 lần thế năng? Trong khi đó có 2? giải thích giúp em.