Cho A=2+22+23+...+260.Chung minh A chia het cho 3,7 va15
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
HH
3
3 tháng 10 2015
A=2+2^2+2^3+...+2^60
A=(2+2^2)+(2^3+2^4)+(2^5+2^6)+...+(2^59+2^60)
A=2(1+2)+2^3(1+2)+2^5(1+2)+...+2^59(1+2)
A=2.3+2^3.3+2^5.3+...+2^59.3
A=3(2+2^3+2^5+...+2^59)
=>A chia hết cho 3
PT
1
CM
14 tháng 5 2019
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích sao cho tổng đó thành tích các thừa số trong đó có một thừa số chia hết cho 7. Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: A = 2 + 2 2 + 2 3 + … + 2 60 = 2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + … + 2 58 + 2 59 + 2 60 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2. 1 + 2 + 2 2 + 2 4 . 1 + 2 + 2 2 + … + 2 58 . 1 + 2 + 2 2 = 2 + 2 4 + … + 2 58 .7 ⇒ A ⋮ 7 |
PT
1
14 tháng 12 2022
a: \(2A=2^2+2^3+...+2^{61}\)
=>A=2^61-2
b: \(A=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(=7\left(2+2^4+...+2^{55}+2^{58}\right)\) chia hết cho 7(1)
\(A=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{59}\left(1+2\right)=3\left(2+2^3+...+2^{59}\right)⋮3\left(2\right)\)
Từ (1), (2) suy ra A chia hết cho 21
TM
1
GR
10 tháng 10 2017
Sửa đề : 2 + 22 + 23 + ... + 260
2 + 22 + 23 + ... + 260 = ( 2 + 22 + 23 + 24 ) + ( 25 + 26 + 27 + 28 ) + .... + ( 257 + 258 + 259 + 260 )
=20. 30 + 24 . 30 + ... + 256 . 30
= ( 20 + 24 + ... + 256) . 2 . 15 \(⋮\)15
NM
2
4 tháng 10 2018
A=210+211+212+213+...+269
=210x1+210x2+212x1+212x2+...+268x1+268x2+268x4
=210x(1+2)+213x(1+2)+...+268x(1+2)
=210x3+213x3+...+268x3
=(210+212+214+...+268)x3
tích trên có hai thừa số.
trong đó có 1 ts là 3.
=>A chia hết cho 3
A=210+211+212+213+...+269
=210x1+210x2+210x4+213x1+213x2+213x4+...+267x1+267x2+267x4
=210x(1+2+4)+213x(1+2+4)+...+267x(1+2+4)
=210x7+213x7+...+267x7
=(210+213+216+...+267)x7
tích trên có hai thừa số.
trong đó có 1 ts là 7.
=>A chia hết cho 7
k nha!
N
8 tháng 10 2018
Kudo shinichi làm đúng nhưng khó hiểu và còn vài lỗi sai:
\(A=\left(2^{10}+2^{11}\right)+\left(2^{12}+2^{13}\right)+...+\left(2^{68}+2^{69}\right)\)
\(A=2^{10}.\left(1+2\right)+2^{12}.\left(1+2\right)+...+2^{68}.\left(1+2\right)\)
\(A=2^{10}.3+2^{12}.3+....+2^{69}.3\)
\(A=3.\left(2^{10}+2^{12}+...+2^{68}\right)⋮3\)
P/S: tự kiêu quá rồi đó Kudo Shinichi à, trên olm có nhiều người giỏi gấp mấy lần bn họ còn chưa nhận mk giỏi toán chưa nói bn nhận mk siêu giỏi -_-", đọc TCN là bt, cấp 1 thì ko khó lên cấp 2, cấp 3 mới hok sâu hơn nhiều :)
AH
Akai Haruma
Giáo viên
29 tháng 10 2023
Lời giải:
$A=(2+2^2+2^3)+(2^4+2^5+2^6)+....+(2^{58}+2^{59}+2^{60})$
$=2(1+2+2^2)+2^4(1+2+2^2)+....+2^{58}(1+2+2^2)$
$=(1+2+2^2)(2+2^4+....+2^{58})$
$=7(2+2^4+....+2^{58})\vdots 7$.
29 tháng 10 2023
A = 2+22+23+...+260
A = 2.(1+2+22) + 24.(1+2+22) + ... + 258.(1+2+22)
A = 2.7+24.7+...+258.7
A= 7. (2+24+...+258) chia hết cho 7
--> A chia hết cho 7 (ĐPCM)
SX
1
28 tháng 2 2022
Đề sai, viết lại thành:
A= 21+22+23+24+...+259+260
Giải:
A=21+22+23+...............+259+260
A=(21+22+23)+...............+(258+259+260)
A=2.(1+2+22)+............+258.(1+2+22)
A=2.7+.......................+258.7
A=(2+24+..............+258).7 ⋮ 7(đpcm)
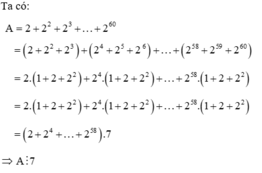
Ta có A = (2+2^2 + 2^3) +...+ (2^58 + 2^59 + 2^60)
A = 2(1+2+2^2) +...+ 2^58(1+2+2^2)
A = 2.7 +... +2^58 . 7
A = 7(2+2^4+...+2^58) chia hết cho 7
Ta lại có A= (2+2^2 + 2^3 +2^4) +( 2^5+2^6+2^7+2^8)+...+(2^57+2^58+2^59+2^60)
A=2(1+2+2^2+2^3) +2^5(1+2+2^2+2^3)+..+2^57(1+2+2^2+2^3)
A= 2.15 + 2^5 . 15 + ...+ 2^57 . 15
A= 15(2+2^5+...+2^57) chai hết cho 15
Do 15 chia hết cho 3 nên A cũng chia hết cho3
Vậy A chia hết cho 3,7,15
A= (2+22)+(23+24)+...+(259+260)
A=2.(1+2)+23.(1+2)+...+259.(1+2)
A=2.3+23.3+...+259.3
A=3.(2+23+...+259)
Vì 3 chia hết cho 3 => 3.(2+23+...+259) chia hết cho 3
=>A chia hết cho 3
A= (2+22+23)+...+(258+259+260)
A=2.(1+2+22)+...+258.(1+2+22)
A=2.7+...+258.7
A=7.(2+...+258)
Vì 7 chia hết cho 7 =>7.(2+...+258) chia hết cho 7
=>A chia hết cho 7
A= (2+22+23+24)+...+(257+258+259+260)
A=2.(1+2+22+23)+...+257.(1+2+22+23)
A=2.15 +...+257.15
A=15.(2+...+257)
vì 15 chia hết cho15=>15.(2+...+25) chia hết cho 15
=>A chia hết cho 15