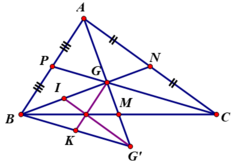
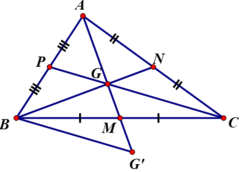
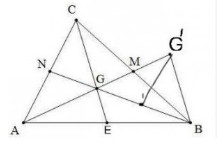
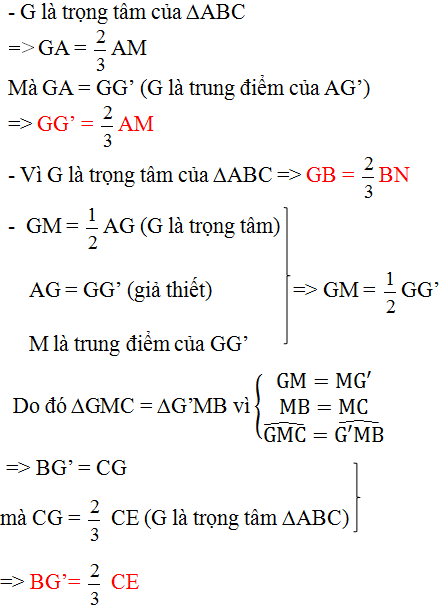
gọi G là trọng tâm của tam giác ABC .trên tia AG lấy điểm G' sao cho G là trung diểm của AG'
a,chứng minh BG'=CG
b,đường trung trực của cạnh BC lần lượt cắt AC,GC,BG'tại i.J,K .chứng minh rằngBK=CJ
c,chứng minh góc ICJ=góc IBJ
giúp mk với mk đg cần gấp .

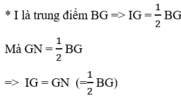
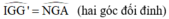
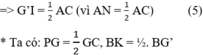

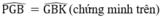
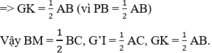
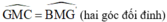
 AM
AM AG ( G là trọng tâm )
AG ( G là trọng tâm )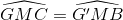
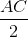
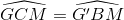 (lại góc sole trong)
(lại góc sole trong) (đồng vị)
(đồng vị)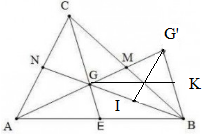


Làm tắt luôn cho nhanh này=,=
a,Gọi D là trug điểm BC
Tam giác BDG'=tam giác CDG(c.g.c)-->BG'=GC
b,Tam giác vuông DBK=tam giác vuông DIC(g.c.g)-->BK=JC
c,BI=IC(I thuộc trung trục BC)
tương tự JC=JB\Rightarrow góc IBJ=góc ICJ(bằng hiệu các góc bằng nhau)