Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bạn ơi đề bài sai nha mik sửa lại đề bài
\(\left(x^3-1\right)\left(x^3+1\right)=\left(x^2-1\right)\left(x^2+x+1\right)\)
VT = \(\left(x^3-1\right)\left(x^3+1\right)=\left(x^3\right)^2-1=x^6-1\)
VP = \(\left(x^2-1\right)\left(x^2+x+1\right)=\left(x^2\right)^3-1=x^6-1\)
Ta thấy VT = VP
=> \(\left(x^3-1\right)\left(x^3+1\right)=\left(x^2-1\right)\left(x^2+x+1\right)\) (đpcm)



x^5- 1/ x-1= x^4+ x^3+ x^2+ x+ 1
<=> x^5 - 1 = (x - 1)(x^4 + x^3 + x^2 + x + 1)
<=> x^5 - 1 = x^5 + x^4 + x^3 + x^2 + x - x^4 - x^3 - x^2 - x - 1
<=> x^5 - 1 = x^5 - 1 (đúng)
=> đpcm
Viết lại cho vui ạ:))
\(\dfrac{x^5-1}{x-1}=x^4+x^3++x^2+x+1\\ \Leftrightarrow x^5-1=\left(x-1\right)\left(x^4+x^3+x+1\right)\\ \Leftrightarrow x^5-1=x^5+x^4+x^3+x^2+x-x^4-x^3-x^2-x-1\\ \Leftrightarrow x^5-1=x^5-1\left(đpcm\right)\)


Bài 1:
1) \(B=1:\dfrac{\left(x+2\right)\left(\sqrt{x}+1\right)+\left(x-1\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+1\right)\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(x+\sqrt{x}+1\right)}{x\sqrt{x}-\sqrt{x}}=\dfrac{\left(x-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(x-1\right)}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
2) \(VT=\dfrac{\left(6a+1\right)\left(a+6\right)+\left(6a-1\right)\left(a-6\right)}{a\left(a-6\right)\left(a+6\right)}.\dfrac{\left(a-6\right)\left(a+6\right)}{a^2+1}\)
\(=\dfrac{12a^2+12}{a\left(a^2+1\right)}=\dfrac{12\left(a^2+1\right)}{a\left(a^2+1\right)}=\dfrac{12}{a}=VP\)

Sửa đề: (x+y)(x+y+2)-2(x+1)(y+1)+2-x^2-y^2
=(x+y)^2+2(x+y)-x^2-y^2-2(xy+x+y+1)+2
=2xy+2(x+y)-2xy-2x-2y-2+2
=2(x+y)-2(x+y)-2+2
=0
=>Đẳng thức được chứng minh
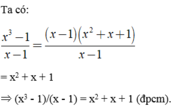
\(\left(x-1\right)\left(x^2+x+1\right)=x^3-1\)
\(VT=x^3+x^2+x-x^2-x-1=x^3-1=VP\) (điều phải chứng minh)