Làm giúp em câu F và G thôi ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(e,\left(x-2\right)^2-16=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\\ f,x^2-5x-14=0\\ \Leftrightarrow\left(x-7\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ g,8x\left(x-3\right)+x-3=0\\ \Leftrightarrow\left(8x+1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{8}\\x=3\end{matrix}\right.\)

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB

1 The gymnast won a total of ten medals at 3 Olympic Games
2 The principal invited a sports star to give a talk at my school yesterday

Mỗi người bạn là một món quà quý giá. Bên bạn bè chúng ta có thật nhiều kỉ niệm. Em có một kỉ niệm thật vui với người bạn thân của mình, đó cũng là kỉ niệm khó quên nhất trong lòng em.
Tham khảoĐó là từ hồi em học lớp hai, hồi đó em và Lan là bạn thân cùng một lớp, hai đứa đi học, đi chơi hay làm gì cũng đều có nhau. Lan thì thích búp bê còn em thì thích đọc sách, đặc biệt là những cuốn truyện thiếu nhi, hai đứa mỗi người mỗi sở thích vậy đó. Em còn nhớ hôm đó là ngày sinh nhật mình, Lan đã dành hết số tiền cậu ấy tiết kiệm được mua tặng em những cuốn truyện hay. Mở món quà ấy ra, em vui và hạnh phúc lắm, Lan là người luôn hiểu và dành cho em nhiều điều tuyệt vời. Trong hộp quà sinh nhật hôm ấy còn có một bức thư có lời chúc mừng sinh nhật kèm lời tạm biệt. Lan bảo, ngày mai bạn ấy phải cùng gia đình chuyển vào Nam sống, những ngày qua cậu ấy cố giấu vì sợ em buồn. Đây là món quà sinh nhật cũng là món quà chia tay, cậu ấy còn hy vọng em sẽ luôn nhớ và viết thư thường xuyên cho cậu ấy. Hôm đó, em vừa vui, vừa buồn. Vui vì món quà dễ thương nhận được, buồn vì phải chia tay người bạn từng gắn bó bấy lâu. Với em, Lan là một người bạn tốt, em luôn trân trọng tình bạn ấy với Lan.
Bây giờ, tuy hai đứa xa nhau về khoảng cách nhưng vẫn thường xuyên hỏi han nhau về học tập cũng như cuộc sống. Cậu ấy vẫn còn nhớ những sở thích ngày xưa ấy và gửi tặng em những cuốn sách hay. Em cảm thấy mình thật may mắn vì có được người bạn như Lan.

a: Xét tứ giác AMHK có
\(\widehat{MAK}=\widehat{AKH}=\widehat{AMH}=90^0\)
Do đó: AMHK là hình chữ nhật
Suy ra: AH=KM(1)
Xét ΔAHC vuông tại H có
\(AM\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AC=MK^2\)

a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AK là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AFKE có
\(\widehat{AFK}=\widehat{AEK}=\widehat{EAF}=90^0\)
Do đó: AFKE là hình chữ nhật
Suy ra: \(AK=FE\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(AE\cdot AB=FE^2\)
c: Ta có: \(AF\cdot AC+AE\cdot AB+KB\cdot KC\)
\(=AK^2+AK^2+AK^2\)
\(=3\cdot AK^2=3\cdot FE^2\)

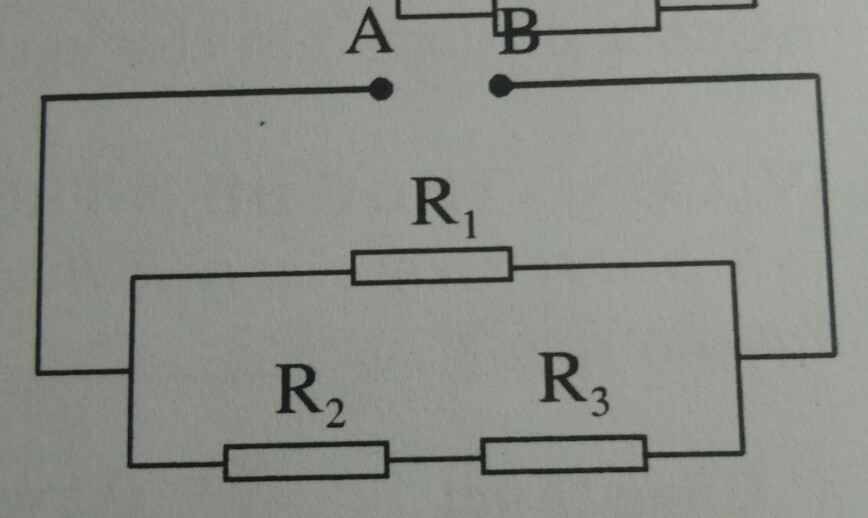
\(a.R_{tđ}=\dfrac{R_1.\left(R_2+R_3\right)}{R_1+R_2+R_3}=\dfrac{6.\left(2+4\right)}{6+2+4}=3\Omega\\ b.U_{AB}=I.R_{tđ}=2.3=6V\\ c.Vì.R_1//R_{23}\Rightarrow U_{AB}=U_1=U_{23}=6V\\ I_1=\dfrac{U_1}{R_1}=\dfrac{6}{6}=1A\\ I_{23}=I-I_1=2-1=1A\\ Vì.R_2ntR_3\Rightarrow I_{23}=I_2=I_3=1A\)









a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKC vuông tại K có KF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AK^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có KA là đường cao ứng với cạnh huyền BC, ta được:
\(KB\cdot KC=AK^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AF\cdot AC=KB\cdot KC\)
b: Xét tứ giác AEKF có
\(\widehat{FAE}=\widehat{AFK}=\widehat{AEK}=90^0\)
Do đó: AEKF là hình chữ nhật
Suy ra: \(AK=EF\left(3\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAKB vuông tại K có KE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AK^2\left(4\right)\)
Từ \(\left(3\right),\left(4\right)\) suy ra \(EF^2=AE\cdot AB\)
c: Ta có: \(AE\cdot AB+AF\cdot AC+KB\cdot KC\)
\(=AH^2+AH^2+AH^2\)
\(=3\cdot EF^2\)