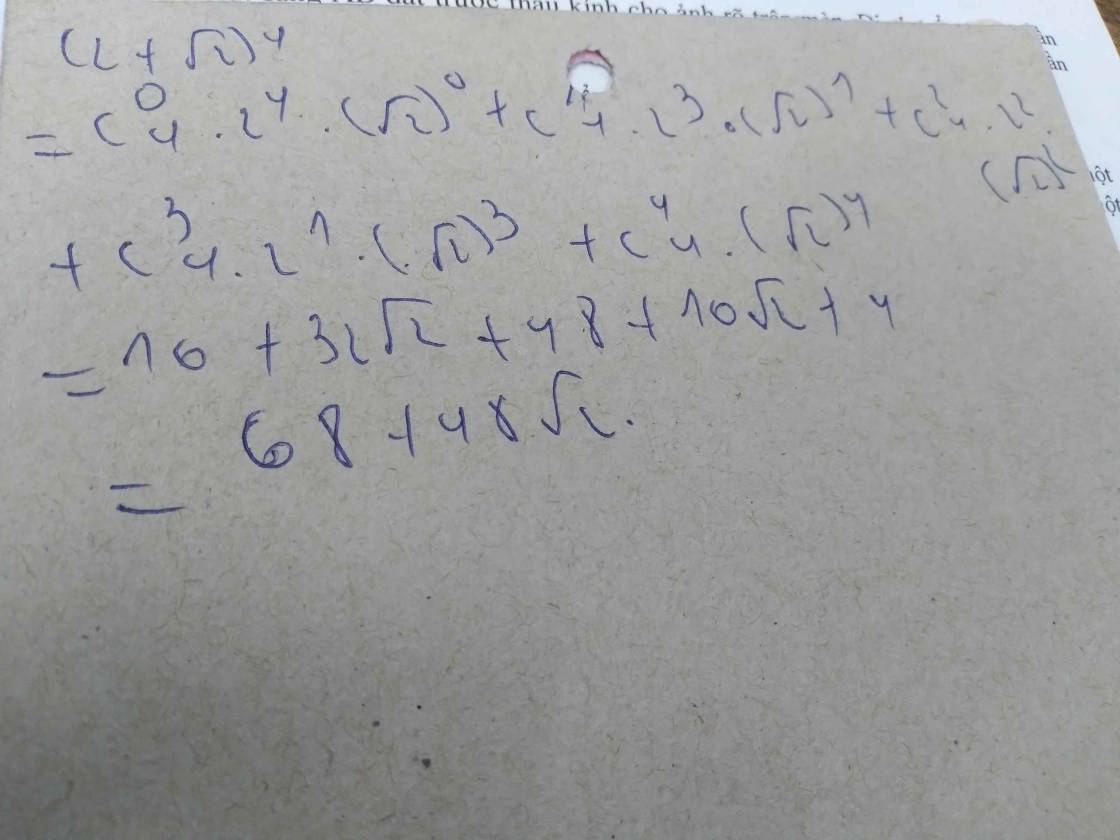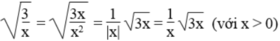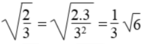rút gọn biểu thức và phá dấu căn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tham khảo:
Điều kiện xác định của phương trình là tập hợp các giá trị của ẩn làm cho tất cả các mẫu trong phương trình đều khác 0. Điều kiện xác định của phương trình viết tắt là ĐKXĐ.

\(x+\frac{1+\sqrt{4x+1}}{2}=\frac{2x+1+\sqrt{4x+1}}{2}=\frac{\left(4x+1\right)+2\sqrt{4x+1}+1}{4}=\left(\frac{1+\sqrt{4x+1}}{2}\right)^2\)
=> \(\sqrt{x+\frac{1+\sqrt{4x+1}}{2}}=\sqrt{\left(\frac{1+\sqrt{4x+1}}{2}\right)^2}=\frac{1+\sqrt{4x+1}}{2}\). tiếp tục n dấu căn
=> A = \(\frac{1+\sqrt{4x+1}}{2}\)

Lời giải:
$\sqrt{(3-\sqrt{3})^2}=|3-\sqrt{3}|=3-\sqrt{3}$ do $3-\sqrt{3}>0$

\(\sqrt{11+6\sqrt{2}}=\sqrt{\left(3+\sqrt{2}\right)^2}=3+\sqrt{2}\)

Biểu thức cần rút gọn : \(\sqrt{x+\sqrt{x+...+\sqrt{x+\frac{1+\sqrt{4x+1}}{2}}}}\) (ĐK : \(x\ge-\frac{1}{4}\))
Ta xét : \(x+\frac{1+\sqrt{4x+1}}{2}=\frac{2x+1+\sqrt{4x+1}}{2}=\frac{4x+1+2\sqrt{4x+1}+1}{4}=\left(\frac{\sqrt{4x+1}+1}{2}\right)^2\)
\(\Rightarrow\sqrt{x+\frac{1+\sqrt{4x+1}}{2}}=\frac{\sqrt{4x+1}+1}{2}\)
Do đó, biểu thức cần rút gọn sẽ bằng với : \(\frac{\sqrt{4x+1}+1}{2}\)