mng giúp em bài này gấp ạaa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1 :
a)
Điện trở tương đương của mạch điện
Rtđ= R1 + R2
= 20 + 20
= 40 (Ω)
Cường độ dòng điện của mạch điện
I = \(\dfrac{U}{R}=\dfrac{12}{40}=0,3\left(A\right)\)
⇒ I = I1 = I2 = 0,3 (A)
b) Điện trở tương đương của mạch điện
Rtđ = \(\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{20.20}{20+20}=10\)(Ω)
Có : U = U1 = U2 = 12V (vì R1 // R2)
I1 = \(\dfrac{U_1}{R_1}=\dfrac{12}{20}=0,6\left(A\right)\)
I2 = \(\dfrac{U_2}{R_2}=\dfrac{12}{20}=0,6\left(A\right)\)
Chúc bạn học tốt
a, Điện trở td khi lấp nối tiếp:
Rtd=R1+R2=40 (Ω)
CĐDĐ khi lấp nối tiếp:
I=\(\dfrac{U}{R_{td}}\)=0,3 A
b, Điện trở td khi lấp song song:
Rtd=\(\dfrac{R_1.R_2}{R_1+R_2}\)=10 (Ω)
CĐDĐ khi lấp song song:
I=\(\dfrac{U}{R_{td}}\)=1,2 A

ĐKXĐ : \(x^4+\left(\sqrt{3}-\sqrt{2}\right).x^2-\sqrt{6}\ne0\)
\(\Leftrightarrow x\ne\sqrt[4]{2}\)
\(P=\dfrac{x^2-\sqrt{2}}{x^4+\left(\sqrt{3}-\sqrt{2}\right).x^2-\sqrt{6}}\)
\(=\dfrac{x^2-\sqrt{2}}{\left(x^4-\sqrt{2}x^2\right)+\sqrt{3}\left(x^2-\sqrt{2}\right)}\)
\(=\dfrac{x^2-\sqrt{2}}{\left(x^2+\sqrt{3}\right)\left(x^2-\sqrt{2}\right)}=\dfrac{1}{x^2+\sqrt{3}}\)


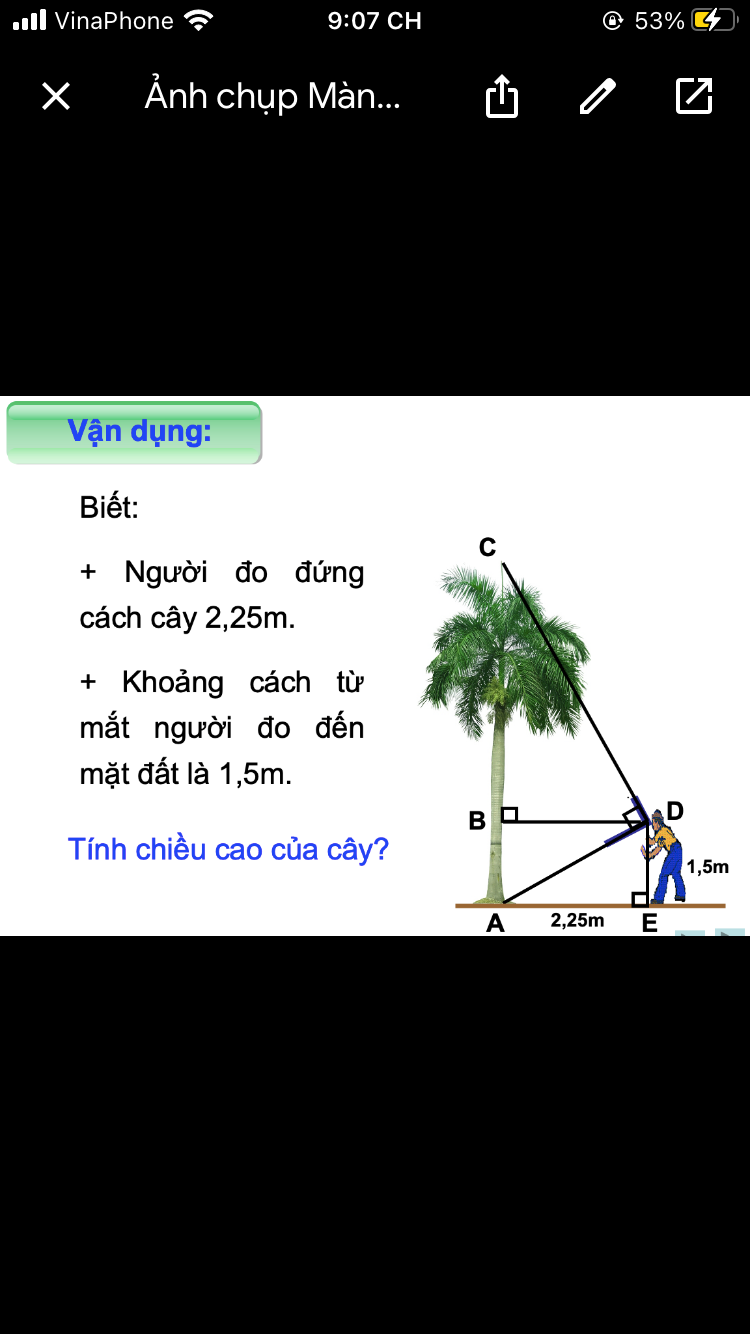
Xét tam giác ADE vuông tại E có:
\(AD^2=AE^2+DE^2\)(định lý Pytago)
\(\Rightarrow AD^2=\dfrac{117}{16}\left(m\right)\)
Xét tam giác ADC vuông tại D có đường cao DB có:
\(AD^2=AB.AC\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow AC=\dfrac{AD^2}{AB}=\dfrac{117}{16}:1,5=\dfrac{39}{8}\left(m\right)\)
Vậy chiều cao của cây là \(\dfrac{39}{8}m\)

=>R1 nt(R2//R3)
\(=>Rtd=R1+\dfrac{R2R3}{R2+R3}=12+\dfrac{8.24}{8+24}=18\Omega\)
\(=>U23=U2=U3=0,4.R23=0,4.\dfrac{8.24}{8+24}=2,4V=>I2=\dfrac{U2}{R2}=\dfrac{2,4}{8}=\dfrac{3}{10}A=>I3=0,4-\dfrac{3}{10}=0,1A\)
\(=>Um=ImRt=0,4.18=7,2V=>U1=U-U12=7,2-2,4=4,8V\)

Câu 2:
uses crt;
var a:array[1..100]of integer;
i,n,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
t:=0;
for i:=1 to n do
if (4<a[i]) and (a[i]<15) then t:=t+a[i];
writeln(t);
readln;
end.

Phương trình hoành độ giao điểm là:
\(x^2-2mx+m^2-m=0\)
a: Để (P) cắt (d) tại hai điểm phân biệt thì \(\left(-2m\right)^2-4\left(m^2-m\right)>0\)
=>4m>0
hay m>0
b: Để (P) cắt (d) tại hai điểm nằm về hai phía của trục tung thì \(m^2-m< 0\)
=>0<m<1








chữa:AB là hai cực nguồn điện
xét TH: K mở =>(R1 nt R2)//(R3 nt R4)
\(=>Uab=U12=U34=24V\)
\(=>I12=I1=I2=\dfrac{U12}{R12}=\dfrac{24}{R1+R2}=\dfrac{24}{12}=2A\)
\(=>I34=I3=I4=\dfrac{U34}{R3+R4}=\dfrac{24}{12}=2A\)
xét TH K đóng =>(R1//R3) nt(R2//R4)(kết quả hơi xấu)
\(=>I13=I24=\dfrac{Uab}{Rtd}=\dfrac{24}{\dfrac{R1.R3}{R1+R3}+\dfrac{R2.R4}{R2+R4}}=\dfrac{24}{\dfrac{4.6}{4+6}+\dfrac{8.6}{8+6}}=\dfrac{70}{17}A\)
\(=>U13=U1=U3=I13.R13=\dfrac{168}{17}V=>I1=\dfrac{\dfrac{168}{17}}{R1}=\dfrac{42}{17}A=>I3=\dfrac{\dfrac{168}{17}}{R3}=\dfrac{28}{17}A\)
làm tương tự đối với U24 để tìm I2,I4
b, (R1 nt R2)//(R3 nt R4) tính Ucd=-U1+U3, tính U1,U3 là xong