Các bạn giúp mình vs ![]()

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Phần a bạn tự làm nha! (Đ/S: 0,5)
b, B = \(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{\sqrt{x}+2}{3-\sqrt{x}}+\dfrac{\sqrt{x}+2}{x-5\sqrt{x}+6}\) với \(x\ge0;x\ne4;x\ne9\)
B = \(\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
B = \(\dfrac{x-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{x-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
B = \(\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
B = \(\dfrac{1}{\sqrt{x}-2}=\dfrac{\sqrt{x}+2}{x-4}\)
Vậy ...
c, Ta có: A = \(1-\dfrac{\sqrt{x}}{\sqrt{x}+1}\)= \(\dfrac{1}{\sqrt{x}+1}\)
T = \(\dfrac{A}{B}\)= \(\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)= 1 - \(\dfrac{3}{\sqrt{x}+1}\)
Ta có: x \(\ge\) 0 \(\Leftrightarrow\) \(\sqrt{x}\ge0\) \(\Leftrightarrow\) \(\sqrt{x}+1\ge1\) \(\Leftrightarrow\) \(\dfrac{3}{\sqrt{x}+1}\le3\) \(\Leftrightarrow\) \(-\dfrac{3}{\sqrt{x}+1}\ge-3\) \(\Leftrightarrow\) T \(\ge\) -2
Vậy ...
Bài 2: ĐK: x \(\ge\) 0
Giả sử: \(P\) < \(\sqrt{P}\)
\(\Leftrightarrow\) \(\dfrac{\sqrt{x}+2}{\sqrt{x}+5}< \dfrac{\sqrt{\sqrt{x}+2}}{\sqrt{\sqrt{x}+5}}\)
\(\Leftrightarrow\) \(\dfrac{\sqrt{\left(\sqrt{x}+2\right)\left(\sqrt{x}+5\right)}-\left(\sqrt{x}+2\right)}{\sqrt{x}+5}>0\)
\(\Leftrightarrow\) \(\sqrt{\left(\sqrt{x}+2\right)\left(\sqrt{x}+5\right)}-\left(\sqrt{x}+2\right)>0\) (\(\sqrt{x}+5>0\) với mọi x \(\ge\) 0)
\(\Leftrightarrow\) \(\sqrt{\left(\sqrt{x}+2\right)}\sqrt{\sqrt{x}+5-\sqrt{x}-2}>0\)
\(\Leftrightarrow\) \(\sqrt{\left(\sqrt{x}+2\right)}\sqrt{3}>0\)
\(\Leftrightarrow\) \(\sqrt{\sqrt{x}+2}>0\)
Vì x \(\ge\) 0 \(\Leftrightarrow\) \(\sqrt{x}+2\ge2\) \(\Leftrightarrow\) \(\sqrt{\sqrt{x}+2}\ge\sqrt{2}>0\) (Đpcm)
Vậy \(P\) < \(\sqrt{P}\)
Chúc bn học tốt!

ĐKXĐ : \(2-x^4\ge0\)
Áp dụng Cô si
\(\sqrt[4]{2-x^4}=\sqrt[4]{\left(2-x^4\right).1.1.1}\le\dfrac{2-x^4+1+1+1}{4}=\dfrac{5-x^4}{4}\)
\(VT\le\dfrac{x^2\left(5-x^4\right)}{4}-x^4+x^3-1=\dfrac{-\left(x-1\right)^2\left(\left(x^2+x\right)^2+6\left(x+\dfrac{2}{5}\right)^2\right)}{4}\le0=VP\)
Dấu "=" \(x=1\)
Vậy S = {1}

III
watching
listening
to buy
to speak
making
eating
working
to call
to built
to do
IV
collection
bird-watching
photography
interesting
Carving
activity
usually
creative




12. In spite of feeling tired, the man tried to finish the work.
13.She swims very well.




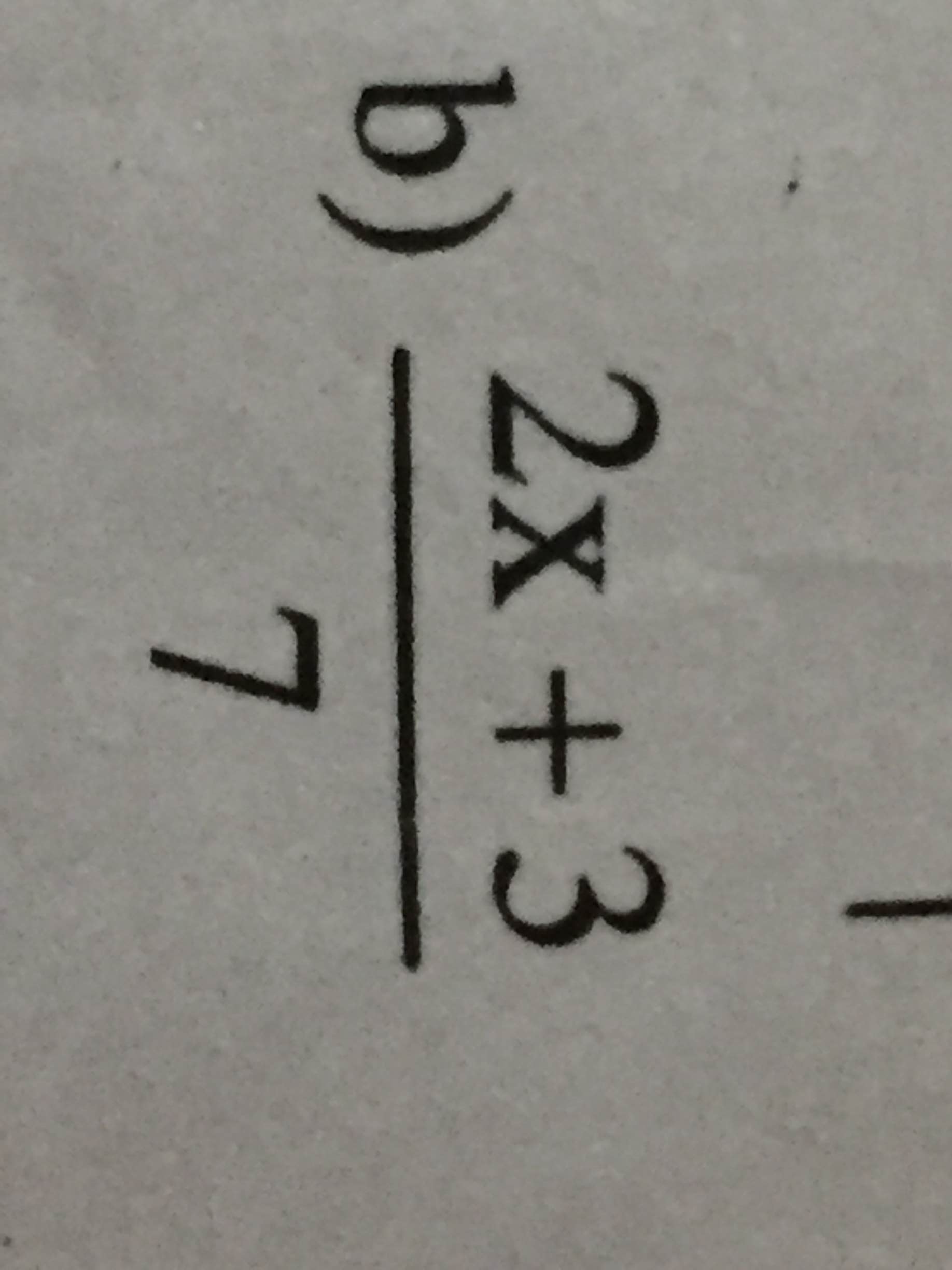




1/ Ta có hình vẽ:
A C B I E F H
a/ Ta có: BE và CF là các đường cao của tam giác ABC.
Mà BE cắt CF tại H
=> H là trực tâm của tam giác
H thuộc AI
=> AI cũng là đường cao của tam giác ABC.
Vì tam giác ABC cân tại A
=> AI cũng là trung tuyến của tam giác
=> I là trung điểm của BC.
b/ Xét hai tam giác vuông ABE và ACF có:
A: góc chung
AB = AC (t/g ABC cân)
=> tam giác ABE = tam giác ACF
=> AE = AF.
Ta có: AB = AC (GT)
==> AB - AF = AC - AE
hay BF = CE
Xét tam giác BFI và tam giác CEI có:
góc B = góc C (t/g ABC cân)
BI = IC (I là trung điểm BC)
BF = CE (cmt)
=> tam giác BFI = tam giác CEI
=> IF = IE
Vậy tam giác IEF cân tại I
Bài 1:
Ta có BE, CF là đường cao TG ABC
=> AI là đường cao thứ 3 của TG ABC
Mà TG ABC cân AI cũng là đường phân giác
=> BAI = CAI
Xét TG ABI và TG ACI
AIB= AIC = 90 độ
AB = AC( TG ABC cân tại A)
BAI= CAI( cmt)
=> TG ABI= TG ACI
=> BI= IC
=> I là trung điểm BC