Phương trình li độ của một vật là x = Acos(4πt + φ) cm. Vào thời điểm t
1 = 0,2 (s) vật có li độ cực đại. Vật sẽ có
li độ cực đại lần kế tiếp vào thời điểm
A. t2 = 0,7 (s). B. t2 = 1,2 (s). C. t2 = 0,45 (s). D. t2 = 2,2 (s).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
18 tháng 3 2019
Chọn D.
Thời gian hai lần liên tiếp gia tốc của vatah có độ lớn cực đại (vật ở vị trí biên) là T/2 nên:
suy ra:
Vận tốc trung bình trong khoảng thời gian này
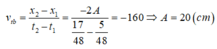
Từ t = 0 đến t 1 = 5 / 48 s phải quét một góc:
Vì tại thời điểm , vật ở biên dương nên từ vị trí này quay ngược lại một góc thì được trạng thái ban đầu và lúc này, pha ban đầu của dao động
H9
HT.Phong (9A5)
CTVHS
14 tháng 6 2023
Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)
VT
24 tháng 11 2019
Đáp án A
Hai thời điểm vuông pha nhau, ta có A = x 1 2 + x 2 2 = 5
VT
16 tháng 10 2017
Đáp án B
Ta để ý rằng hai thời điểm t 1 và t 2 vuông pha nhau
Tại thời điểm t 1 vật có li độ x = - 6 cm và chuyển động theo chiều dương x 2 = 8 cm
Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=0,5s\)
Li độ cực đại kế tiếp cách nhau 1 chu kì dao động.
Như vậy, thời điểm kế tiếp li độ đạt cực đại là: \(t_2=0,2+0,5=0,7s\)