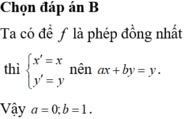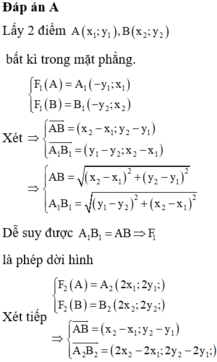Trong mặt phẳng Oxy xét phép biến hình F biến mỗi điểm \(M\left(x;y\right)\) thành \(M'\left(2x-1;-2y+3\right)\). Chứng minh F là một phép đồng dạng ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
24 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
CM
12 tháng 6 2018
Lấy điểm N ( x 1 ; y 1 ) , thì điểm N ′ ( 2 x 1 − 1 ; − 2 y 1 + 3 ) = F ( N ) . Ta có
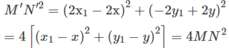
Từ đó suy ra với hai điểm M, N tùy ý và M', N' lần lượt là ảnh của chúng qua F ta có M′N′ = 2MN. Vậy F là phép đồng dạng với tỉ số đồng dạng là 2.
24 tháng 8 2016
phép dời hình là phép biến điểm thành điểm tia thành tia đoạn thẳng thành đoạn thẳng bằng nó, đừong tròn thành đường tròn cùng bán kính...........(trong sgk định nghĩa ý)
phép dời hình koh làm thay đổi khoảng cách của 2 điểm bất kì
dễ dàng thấy khoảng cách OM và OM' trong phép biến F1 là bằng nhau
con trong phép 2 thì khác nhau nó làm thay đổi khoảng cách nên không là phép biến hình còn nếu muốn tổng quát thì chon điểm n(x1;y1) bất kì rùi so sánh khoảng cách NM và NM'
CM
23 tháng 12 2019
Đáp án A
Chọn A(–3; 1) ⇒ F ( A ) = A ' ( − 8 ; − 4 )
B(3;–3) ⇒ F ( B ) = B ' ( 16 ; − 2 )
Phương trình đường thẳng (d) đi qua 2 điểm A’, B’: 1 12 x − 10 3 = y
24 tháng 8 2016
a) Gọi M' (x₁' ; y₁' ), N' (x₂' ; y₂ )
* M' là ảnh của M qua phép F, nên toạ độ M' thoả:
{x₁' = x₁.cosα – y₁.sinα + a
{y₁' = x₁.sinα + y₁.cosα + b
* N' là ảnh của N qua phép F, nên toạ độ N' thoả:
{x₂' = x₂.cosα – y₂.sinα + a
{y₂' = x₂.sinα + y₂.cosα + b
b) * Khoảng cách d giữa M và N là:
d = MN = √ [(x₂ - x₁)² + (y₂ - y₁)²]
* Khoảng cách d' giữa M' và N' là:
d' = M'N' = √ [(x₂' - x₁' )² + (y₂' - y₁' )²]
= √ {[x₂.cosα – y₂.sinα + a - (x₁.cosα – y₁.sinα + a)]² + [x₂.sinα + y₂.cosα + b - (x₁.sinα + y₁.cosα + b)]²}
= √ {[cosα(x₂ - x₁) - sinα(y₂ - y₁)]² + [sinα(x₂ - x₁) + cosα(y₂ - y₁)]²}
= √ [(x₂ - x₁)².(cos²α + sin²α) + (y₂ - y₁)².(cos²α + sin²α)]
= √ [(x₂ - x₁)² + (y₂ - y₁)²]
c) Phép F là phép dời hình vì: MN = M'N' = √ [(x₂ - x₁)² + (y₂ - y₁)²]
d) Khi α = 0 ⇒ cosα = 1, sinα = 0
Suy ra:
{x' = x + a
{y' = y + b
Đây là biểu thức toạ độ của phép tịnh tiến. Vậy F là phép tịnh tiến
CM
14 tháng 11 2018
Chọn B.
Phương pháp: Phép đồng nhất thì M phải trùng với M' với mọi M.
Cách giải: Dễ thấy a = 0; b = 1