Cho hình bs.4.
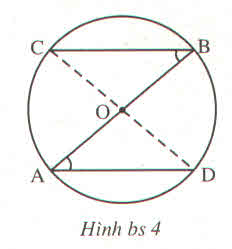
Chứng minh rằng :
a) C, O, D thẳng hàng
b) BC = AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 9 2018
+) Xét tam giác OAD có: OA = OD (= bán kính đường tròn)
Suy ra tam giác OAD cân tại O.
Suy ra: ∠A = ∠D ( tính chất tam giác cân). (1)
+) Xét tam giác OBC có: OB = OC (= bán kính đường tròn)
Suy ra tam giác OBC cân tại O.
Suy ra: ∠B = ∠C ( tính chất tam giác cân). (2)
+) Lại có: ∠A = ∠B ( giả thiết) (3)
Từ (1); (2) và (3) suy ra: ∠A = ∠B = ∠C = ∠D
Vậy hai tam giác cân OAD và OBC có góc ở đáy bằng nhau nên góc ở đỉnh bằng nhau: ∠AOD = ∠BOC (4).
+) Ta có: ∠AOD + ∠DOB = 180º ( hai góc kề bù) (5)
Từ (4) và (5) suy ra: ∠BOC + ∠DOB = 180º hay 3 điểm C, O và D thẳng hàng.
CM
9 tháng 2 2019
Xét tam giác OAD và ∆ OCB có:
OA = OC ( = bán kính đường tròn)
∠AOD = ∠BOC ( hai góc đối đỉnh)
OD = OB ( = bán kính đường tròn)
Suy ra:∆ OAD = ∆ OCB ( c.g.c)
Suy ra: AD = BC ( hai cạnh tương ứng).
A
1
2 tháng 10 2021
a: Ta có: \(\widehat{EAB}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AE//BC
Ta có: \(\widehat{DAC}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
b: Ta có: AE//BC
AD//BC
mà AD và AE có điểm chung là A
nên D,A,E thẳng hàng
CM
10 tháng 5 2019
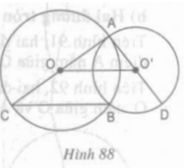
a) Hai đường tròn (O) và (O’) cắt nhau
b) Xét tam giác ABC có:
OA = OB = OC = bán kính đường tròn (O)
Mà BO là trung tuyến của tam giác ABC
⇒ ∆ABC vuông tại B ⇒ AB ⊥ BC (1)
Lại có OO’ là đường trung trực của AB
⇒ AB ⊥ OO' (2)
Từ (1) và (2) ⇒ OO’ // BC
Chứng minh tương tự ta có ∆ABD vuông tại B ⇒ AB ⊥ BD (3)
Từ (1) và (3) ⇒ B, C, D thẳng hàng.
a) Các tam giác cân AOD , BOC có góc đáy bằng nhau nên góc ở đỉnh bằng nhau: \(\widehat{AOD}\) = \(\widehat{BOC}\) . Ta lại có : góc AOD + góc BOD = 180o nên\(\widehat{BOC}\) + \(\widehat{BOD}\) = 180o
Vậy C ,O ,D thẳng hàng
b) Xét tam giác BOC = tam giác AOD (g.c.g)
=> BC = AD (2.c.t.ư)