Giải giùm mình câu 44 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Thể tích của vật là
`V_v = V_2-V_1 =175-130=45cm^3=4,5*10^(-5)m^3`
Do vật chìm hoàn toàn trong nước nên
Lực đẩy Ác si met t/d lên vật là
`F_A = V_v * d_n =4,5*10^(-5) *10000 =0,45(N)`
khối lg của vật ngoài ko khí là
`m=P/10=(P_n +F_A )/10= (4,2+0,45)/10 =0,465(kg)`
khối lg riêng vật là
`D=m/V_v = (0,465)/(4,5*10^(-5))=~~ 10333,3(kg//m^3)`


a.
Kéo dài AB và DC cắt nhau tại E
Trong mp (SCD), nối EM kéo dài cắt SD tại F
\(\Rightarrow\) Tứ giác ABMF là thiết diện của (BAM) và chóp
b.
Trong mp (SCD), nối MN kéo dài cắt SE tại P ( điểm E được dựng ở câu a)
Trong mp (SAB), nối AP cắt SB tại Q
\(\Rightarrow\) Tứ giác ANMQ là thiết diện của (MAN) và chóp

3)\(sin6x.sin2x=sin5x.sinx\)
\(\Leftrightarrow\dfrac{1}{2}\left(cos4x-cos8x\right)=\dfrac{1}{2}\left(cos4x-cos6x\right)\)
\(\Leftrightarrow cos8x=cos6x\)
\(\Leftrightarrow\left[{}\begin{matrix}8x=6x+k2\pi\\8x=-6x+k2\pi\end{matrix}\right.\) (\(k\in Z\)) \(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{k\pi}{7}\end{matrix}\right.\)(\(k\in Z\))
Vậy...
13)\(cosx.cos3x-sin2x.sin6x-sin4x.sin6x=0\)
\(\Leftrightarrow\dfrac{1}{2}.\left(cos2x+cos4x\right)-\dfrac{1}{2}\left(cos4x-cos8x\right)-\dfrac{1}{2}\left(cos2x-cos10x\right)=0\)
\(\Leftrightarrow cos8x+cos10x=0\)
\(\Leftrightarrow2.cos9x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos9x=0\\cosx=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{18}+\dfrac{k\pi}{9}\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\) (\(k\in Z\))
Vậy...

Câu 15:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
DO đó: ΔADF=ΔEDC
Suy ra: DF=DC
c: Ta có: ΔBFC cân tại B
mà BD là phân giác
nên BD là đường cao

Lời giải:
Để pt có 2 nghiệm pb thì $\Delta'=1-(m-1)>0\Leftrightarrow m< 2$
Áp dụng hệ thức Viet:
$x_1+x_2=2$
$x_1x_2=m-1$
Khi đó:
$x_1^2+x_2^2-3x_1x_2=2m^2+|m-3|$
$\Leftrightarrow (x_1+x_2)^2-5x_1x_2=2m^2+|m-3|$
$\Leftrightarrow 2^2-5(m-1)=2m^2+|m-3|$
$\Leftrightarrow 2m^2+5m+|m-3|-9=0$
$\Leftrightarrow 2m^2+5m+3-m-9=0$ (do $m< 2 < 3$)
$\Leftrightarrow 2m^2+4m-6=0$
$\Leftrightarrow m^2+2m-3=0$
$\Leftrightarrow (m-1)(m+3)=0$
$\Rightarrow m=1$ hoặc $m=-3$ (đều tm)

Pt có 2 nghiệm khi: \(\left\{{}\begin{matrix}m\ne0\\\Delta'=9\left(m-1\right)^2-9m\left(m-3\right)\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne0\\m\ge-1\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{6\left(m-1\right)}{m}\\x_1x_2=\dfrac{9\left(m-3\right)}{m}\end{matrix}\right.\)
\(x_1+x_2=x_1x_2\Rightarrow\dfrac{6\left(m-1\right)}{m}=\dfrac{9\left(m-3\right)}{m}\)
\(\Rightarrow6\left(m-1\right)=9\left(m-3\right)\)
\(\Rightarrow m=7\)
A đúng






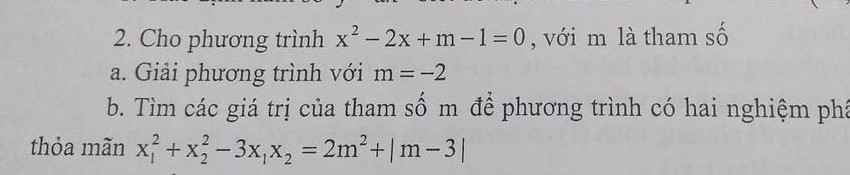


+) Xét phương trình mặt cầu (C):
\(x^2+y^2+z^2-2x-4y-4z=7\\ \Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2+\left(z-2\right)^2=16\)
(C) có tâm I(1;2;2) và có bán kính R=4
+) Xét mặt phẳng (P): \(2x+3y+6z-T=0\)
Điểm M là giao điểm của (C) và (P)!
+) Ta có:
\(IM=\dfrac{\left|2x_M+3y_M+6z_M-T\right|}{\sqrt{2^2+3^2+6^2}}=\dfrac{\left|20-T\right|}{7}\)
Mà: \(0\le IM\le R\Leftrightarrow0\le\dfrac{\left|20-T\right|}{7}\le4\)
Từ đây tìm ra được: \(maxT=48\Leftrightarrow IM=R=4\)
(T max khi và chỉ khi mặt cầu C tiếp xúc mặt phẳng P)
Chọn C
.