Trên hình 49 :
Ax song song với By. \(\widehat{CAx}=50^0,\widehat{CBy}=40^0\). Tính \(\widehat{ACB}\) bằng cách xem nó là góc ngoài của một tam giác ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 1 2017
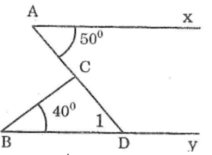
Kéo dài AC cắt By tại D
Vì By // Ax suy ra ∠(D1) = ∠A (hai góc so le trong)
Mà ∠A = 50o(gt) nên ∠(D1) = 50o
TrongΔBCD ta có ∠(ACB) là góc ngoài tại đỉnh C
⇒∠(ACB) = ∠B + ∠(D1) (tính chất góc ngoài của tam giác)
⇒∠(ACB) = 40o + 50o = 90o
Kẻ CD là tia đối của tia CA sao cho D \(\in\) By
Ta có Ax // By (theo đề bài)
^ ^
=> A = CDB = 50° (2 góc so le trong)
Ta có ^ACB = ^B + ^CDB (theo tính chất góc ngoài của một tam giác)
Hay ^ACB= 40° + 50°
^ACB = 90°