So sánh các cạnh của một tam giác cân, biết rằng nó có một góc ngoài bằng \(40^0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo giả thiết, tam giác cân này có một góc ngoài bằng 40o nên nó có một góc trong bằng 180o - 40o = 140o. Góc trong này không thể là góc ở đáy của tam giác cân mà phải là góc ở đỉnh. Vậy cạnh đáy của tam giác cân lớn hơn hai cạnh bên của nó.

Gọi tam giác đó là ΔABC cân tại A
Trường hợp 1: Góc ở đáy bằng 400
hay \(\widehat{B}=\widehat{C}=40^0\)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{A}=180^0-2\cdot\widehat{B}\)(Số đo của góc ở đỉnh trong ΔBAC cân tại A)
hay \(\widehat{A}=100^0\)
Xét ΔABC có \(\widehat{A}>\widehat{B}=\widehat{C}\)(\(100^0>40^0=40^0\))
mà cạnh đối diện của góc A là BC
cạnh đối diện của góc B là AC
cạnh đối diện của góc C là AB
nên BC>AC=AB(Định lí quan hệ giữa góc và cạnh đối diện trong tam giác)
Trường hợp 2: Góc ở đỉnh bằng 400
hay \(\widehat{A}=40^0\)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{B}=\widehat{C}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của các góc ở đáy trong ΔABC cân tại A)
hay \(\left\{{}\begin{matrix}\widehat{B}=70^0\\\widehat{C}=70^0\end{matrix}\right.\)
Xét ΔABC có \(\widehat{B}=\widehat{C}>\widehat{A}\)(\(70^0=70^0>40^0\))
mà cạnh đối diện của góc B là AC
cạnh đối diện của góc C là AB
cạnh đối diện của góc A là BC
nên AC=AB>BC(Định lí quan hệ giữa góc và cạnh đối diện trong tam giác)

c) Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{B}+\widehat{C}=180^0-40^0=140^0\)
Ta có: \(\widehat{B}:\widehat{C}=3:4\)(gt)
nên \(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}\)
mà \(\widehat{B}+\widehat{C}=140^0\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}=\dfrac{\widehat{B}+\widehat{C}}{3+4}=\dfrac{140^0}{7}=20^0\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{\widehat{B}}{3}=20^0\\\dfrac{\widehat{C}}{4}=20^0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{B}=60^0\\\widehat{C}=80^0\end{matrix}\right.\)
Xét ΔABC có \(\widehat{A}< \widehat{B}< \widehat{C}\left(40^0< 60^0< 80^0\right)\)
mà cạnh đối diện với \(\widehat{A}\) là cạnh BC
cạnh đối diện với \(\widehat{B}\) là cạnh AC
và cạnh đối diện với \(\widehat{C}\) là cạnh AB
nên BC<AC<AB

a: góc BAC=180-120=60 độ
góc ABE=70/2=35 độ
góc AEB=180-60-35=85 độ
b: góc ABE<góc BAE<góc AEB
=>AE<BE<AB
c: góc ECB=180-70-60=50 độ
góc BEC=180-85=95 độ
Vì góc EBC<góc ECB<góc BEC
nên EC<EB<BC

Bài toán 2: Cho tam giác ABC cân ở A có chu vi bằng 16cm, cạnh đáy BC = 4cm. So sánh các góc của tam giác ABC.
Tam giác ABC cân tại A (gt). => Góc B = Góc C (Tính chất tam giác cân).
Ta có: Tam giác ABC cân ở A có chu vi bằng 16cm, cạnh đáy BC = 4cm (gt).
=> AB = AC = (16 - 4) : 2 = 6 (cm).
Xét tam giác ABC cân tại A:
Ta có: AB > BC (AB = 6 cm; BC = 4cm).
=> Góc C > Góc A.
Vậy trong tam giác ABC có Góc B = Góc C > Góc A.

Lời giải:
a) Gọi ABC là tam giác cân đã cho và góc ở đỉnh A bằng 40o. Ta có:
a) Gọi ABC là tam giác cân đã cho và góc ở đỉnh A bằng 40o. Ta có:
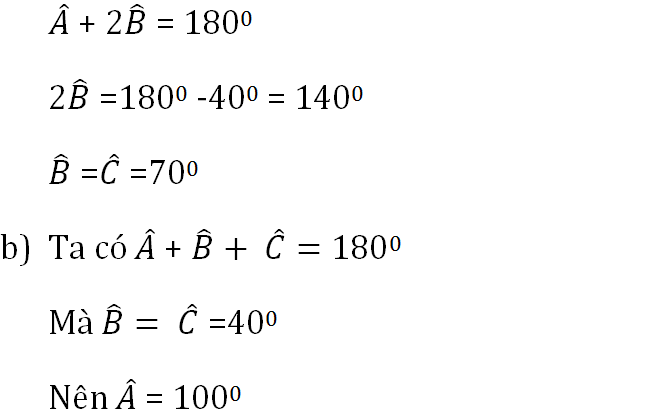
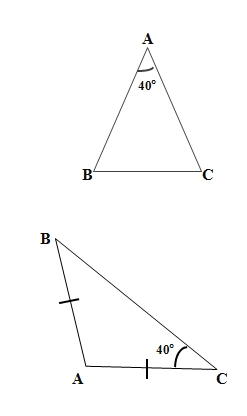

a, giả sử tam giác ABC cân tại A có góc A=40
áp dụng định lý tổng 3 góc trong 1 tam giác ta có
góc A+góc B+góc C=180
hay 40+2.góc B=180
2.góc B=180-40
2.góc B=140
góc B=140:2=70 độ
Vậy 2 góc ở đáy =70 độ
b. giả sử tam giác ABC cân tại A có góc ở đáy =40 độ
Áp dụng định lý tổng 3 góc trong 1 tam giác ta có:
góc A+góc B+góc C=180
hay góc A+40+40=180
gocsA=180-80
góc A=100 độ
vậy góc ở đỉnh =100 độ
a) Gọi ABC là tam giác cân đã cho và góc ở định =400
Ta có +2
=1800
2= 1800 -
= 1400
=> = 700
b) Ta có: +
+
=1800
mà =
=400
nên +2
=1800
+800 =1800
=400
So sánh các cạnh của một tam giác cân, biết rằng nó có một góc ngoài bằng 40o