CMR (1/căn(n^2+1)+1/căn(n^2+2)+...+1/căn(n^2+n)<1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đặt \(S=\frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+...+\frac{1}{\sqrt{n^2+n}}\)
\(n^2+1< n^2+2< ...< n^2+n\)
\(\Rightarrow\frac{1}{\sqrt{n^2+1}}>\frac{1}{\sqrt{n^2+2}}>...>\frac{1}{\sqrt{n^2+n}}\)
\(\Rightarrow\frac{n}{\sqrt{n^2+1}}>\frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+...+\sqrt{n^2+n}\)
\(\frac{n}{\sqrt{n^2+n}}< \frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+n}}+...+\frac{1}{\sqrt{n^2+n}}\)
\(\Rightarrow\frac{n}{\sqrt{n^2+n}}< S< \frac{n}{\sqrt{n^2+1}}\)
Mà \(lim\frac{n}{\sqrt{n^2+1}}=lim\frac{n}{\sqrt{n^2+n}}=1\)
\(\Rightarrow lim\left(S\right)=1\) theo nguyên lý kẹp

Bài 6:
Để B là số nguyên thì \(\sqrt{x}-2+3⋮\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}-2\in\left\{1;-1;3\right\}\)
hay \(x\in\left\{9;1;25\right\}\)

Chụp ảnh hoặc sử dụng gõ công thức nhé bạn. Để vầy khó hiểu lắm


\(lim\frac{\sqrt{9n^2+2n}+n-2}{\sqrt{4n^2+1}}=lim\frac{\sqrt{9+\frac{2}{n}}+1-\frac{2}{n}}{\sqrt{4+\frac{1}{n^2}}}=\frac{\sqrt{9}+1}{\sqrt{4}}=2\)
\(lim\frac{n}{\sqrt{4n^2+2}+\sqrt{n^2}}=lim\frac{1}{\sqrt{4+\frac{2}{n^2}}+\sqrt{1}}=\frac{1}{\sqrt{4}+\sqrt{1}}=\frac{1}{3}\)
\(lim\frac{\sqrt{4n+2}-\sqrt{2n-5}}{\sqrt{n+3}}=lim\frac{\sqrt{4+\frac{2}{n}}-\sqrt{2-\frac{5}{n}}}{\sqrt{1+\frac{3}{n}}}=\frac{2-\sqrt{2}}{1}=2-\sqrt{2}\)
l\\(lim\frac{\sqrt{4n^2+n+1}-n}{n^2+2}=lim\frac{\sqrt{4+\frac{1}{n}+\frac{1}{n^2}}-1}{n+\frac{2}{n}}=\frac{1}{\infty}=0\)
\(lim\frac{\sqrt{9n^2+n+1}-2n}{3n^2+2}=\frac{\sqrt{9+\frac{1}{n}+\frac{1}{n^2}}-2}{3n+\frac{2}{n}}=\frac{1}{\infty}=0\)
Muốn giúp bạn lắm mà ko sao dịch được đề :D
Bạn sử dụng công cụ gõ công thức, nó ở ngoài cùng bên trái khung soạn thảo, chỗ khoanh đỏ ấy, cực dễ sử dụng

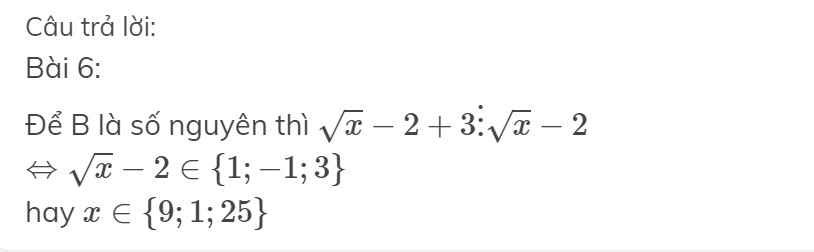
\(\frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+...+\frac{1}{\sqrt{n^2+n}}\)
\(< \frac{1}{\sqrt{n^2}}+\frac{1}{\sqrt{n^2}}+...+\frac{1}{\sqrt{n^2}}\)(\(n\)số hạng)
\(=\frac{n}{\sqrt{n^2}}=1\)
Ta có đpcm.