Chứng minh rằng 51994 + 51993 - 51992 chia hết cho 29
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 9 2016
mk cung dang mac bai nay nen mong nhieu bn giup do chi nha !
N
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
23 tháng 8 2021
\(\overline{abcd}=1000a+100b+10c+d=\)
\(=\left(986a+87b\right)+\left(14a+13b+10c+d\right)=\)
\(=\left(34.29.a+3.29.b\right)+\left(14a+13b+10c+d\right)=\)
\(=29\left(34a+3b\right)+\left(14a+13b+10c+d\right)⋮29\)
Mà \(29\left(34a+3b\right)⋮29\Rightarrow14a+3b+10c+d⋮29\)
\(\Rightarrow2\left(14a+13b+10c+d\right)=28a+26b+20c+2d⋮29\)
\(\Rightarrow28a+26b+20c+2d-29\left(a+b+c+d\right)=\)
\(=-3a-3b-9c-27d=-\left(a+30+9c+27d\right)⋮29\)
\(\Rightarrow a+3b+9c+27d⋮29\)
1 tháng 1 2017
A)...32a+7b=29a+3a+7b
29a tất nhiên chia hết cho 29: 3a+7b chia hết ho 29=>đpcm
b)3a+7b+29b lập luân (a)=>đpcm
c)2(3a+7b)+29a+29 a=>đpvm
d)
NV
0
VD
14 tháng 7 2018
7)a) abcabc : abc = 1001
abcabc = 1001 x abc . Mà 1001 chia hết cho 7; 11; 13 nên 1001 x abc chia hết cho 7; 11; 13 . Vậy abcabc chia hết cho 7; 11; 13 ( đpcm)
b .Vì abc = 2 . deg nên abcdeg : deg = 2001
abcdeg = 2001 x deg. Do 2001 chia hết cho 23 và 29 nên 2001 x deg chia hết cho 23 và 29 . Vậy abcdeg chia hết cho 23 và 29 ( đpcm)
5 tháng 11 2018
Ta có :
abcabc = 1000abc + abc
= 1001 . abc
= 7 . 11 . 13 . abc chia hết cho 7 ; 11 ; 13
PT
1
CM
24 tháng 8 2019
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: 2 9 + 4 2 . 2 5 .2 3 = 2 9 + 2 4 . 2 5 .2 3 = 2 4 2 5 + 1 . 2 5 .2 3 = 2 4 .33. 2 5 .2 3 ⇒ 2 9 + 4 3 . 2 5 .2 3 ⋮ 11 |
PT
1
PT
1
CM
7 tháng 5 2019
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: 2 9 − 4 3 . 2 5 .2 3 = 2 9 − 2 6 . 2 5 .2 3 = 2 6 2 3 − 1 . 2 5 .2 3 = 2 6 . 8 − 1 . 2 5 .2 3 = 2 6 .7. 2 5 .2 3 ⇒ 2 9 − 4 3 . 2 5 .2 3 ⋮ 7 |
PT
1
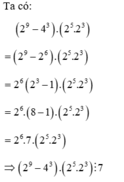
51994 + 51993 - 51992 =51992(52+5-1)=51992.29 chia het cho 29
=> 51994 + 51993 - 51992 chia hết cho 29
=\(5^{1992}\left(5^2+5-1\right)\)
=\(5^{1992}\cdot29\)
mà 29 chia hết cho 29 => \(5^{1992}\cdot29\) chia hết cho 29
Vậy ....