Cho hình chóp tứ giác đều (h.146).

Xem hình và điền số thích hợp vào các ô trống còn ở bảng sau :

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



| a | 6 | 16 | 24 | 32 | 16 |
| d | 5 | 10 | 15 | 20 | 17 |
| h | 4 | 6 | 9 | 12 | 15 |
| Diện tích đáy | 36 | 256 | 576 | 1024 | 256 |
| Diện tích xung quanh | 60 | 320 | 720 | 1280 | 544 |
| Diện tích toàn phần | 96 | 576 | 1296 | 2304 | 800 |
| Thể tích | 48 | 512 | 1728 | 4096 | 1280 |

| Chóp tam giác đều | Chóp tứ giác đều | Chóp ngũ giác đều | Chóp lục giác đều | |
| Đáy | Tam giác đều | Hình vuông | Ngũ giác đều | Lục giác đều |
| Mặt bên | Tam giác cân | Tam giác cân | Tam giác cân | Tam giác cân |
| Số cạnh đáy | 3 | 4 | 5 | 6 |
| Số cạnh | 6 | 8 | 10 | 12 |
| Số mặt | 4 | 5 | 6 | 7 |

| Chiều cao (h) | 8 | 15 | 189 | 11 |
| Trung đoạn (l) | 10 | 17 | 15 | 6 |
| Cạnh đáy | 12 | 16 | 12 | 10 |
| S x q | 240 | 544 | 360 | 120 |

| a | 9 | 35 | 20 | 63 | 28 |
| b | 40 | 12 | 21 | 16 | 45 |
| c | 41 | 37 | 29 | 65 | 53 |
| d | 8 | 18 | 17 | 24 | 13 |
| Diện tích một đáy | 180 | 210 | 210 | 504 | 630 |
| Diện tích xung quanh | 720 | 1512 | 1190 | 3456 | 1638 |
| Diện tích toàn phần | 1080 | 1932 | 1610 | 4464 | 2898 |
| Thể tích | 1440 | 3780 | 3570 | 12096 | 8190 |

a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4
b) Diện tích mỗi mặt tam giác là 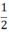 . 4.6 = 12 cm2.
. 4.6 = 12 cm2.
c) Diện tích đáy của hình chóp đều là 4.4 = 16 cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là 12.4 = 48 cm2.

a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là 4
b) Diện tích mỗi mặt tam giác là 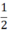 . 4.6 = 12 cm2.
. 4.6 = 12 cm2.
c) Diện tích đáy của hình chóp đều là 4.4 = 16 cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là 12.4 = 48 cm2.

Trước hết ta chứng minh hệ thức: DA2 = AB2 + BC2 + CD2.
+ ΔBCD vuông tại C suy ra: BD2 = BC2 + CD2 .
+ ΔABD vuông tại B ⇒ AD2 = AB2 + BD2
Mà BD2 = BC2 + CD2 ⇒ AD2 = AB2 + BC2 + CD2 .
Vậy AD2 = AB2 + BC2 + CD2 .
Áp dụng hệ thức trên để tính các cạnh còn thiếu trong bảng ta có:
+ Cột 1: AB = 6; BC = 15; CD = 42
⇒AD2 = AB2 + BC2 + CD2 = 62 + 152 + 422 = 2025
⇒AD = 45.
+ Cột 2: AB = 13; BC = 16; AD = 45
⇒CD2 = AD2 - AB2 - BC2 = 452 - 132 - 162 = 1600
⇒CD = 40.
+ Cột 3: AB = 14; CD = 70; DA = 75
⇒BC2 = DA2 - CD2 - AB2 = 752 - 702 - 142 = 529
⇒BC = 23
+ Cột 4: BC = 34; CD = 62; DA = 75
⇒AB2 = DA2 - BC2 - CD2 = 752 - 342 - 622 = 625
⇒AB = 25.
Vậy ta có kết quả như bảng sau:
| AB | 6 | 13 | 14 | 25 |
| BC | 15 | 16 | 23 | 34 |
| CD | 42 | 40 | 70 | 62 |
| DA | 45 | 45 | 75 | 75 |