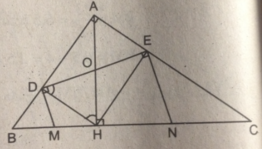
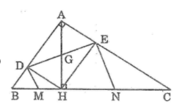
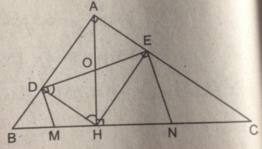
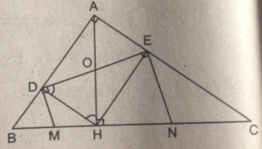
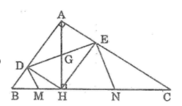
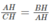Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9 cm
Gọi D và E là hình chiếu của H trên AB và AC
a) Tính độ dài DE
b) Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N. Chứng minh M là trung điểm của BF, N là trung điểm của CH
c) Tính diện tích tứ giác DENM