Cho hàm số y = ( k - 3 )x + k' ( d ) . Tìm các giá trị của k và k' để đường thẳng ( d ) thỏa mãn một trong các điều kiện sau
a. Đi qua điểm A( 1 ; 2 ) và B( -3 ; 4 )
b. Cắt trục tung tại điểm có tung độ bằng 1-\(\sqrt{2}\) và cắt trục hoành tại điểm 1 + \(\sqrt{2}\)
c. Cắt đường thẳng 2y - 4x + 5 = 0
d. Song song với đường thẳng y - 2x -1 =0
e. Trùng với đường thẳng 3x + y - 5 = 0

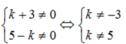
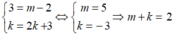
a: Đặt a=k; b=k'
=>(d): y=(a-3)x+b
Vì (d) đi qua A(1;2) và B(3;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-3+b=2\\3\left(a-3\right)+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\3a+b=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=1\\a=4\end{matrix}\right.\)
b: (d): y=(a-3)x+b
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}b=1-\sqrt{2}\\\left(a-3\right)\cdot\left(1+\sqrt{2}\right)=\sqrt{2}-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=1-\sqrt{2}\\a=6-2\sqrt{2}\end{matrix}\right.\)
d: y-2x-1=0
nên y=2x+1(d1)
(d): y=(a-3)x+b
Để (d)//(d1) thì \(\left\{{}\begin{matrix}a-3=2\\b< >1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=5\\b< >1\end{matrix}\right.\)