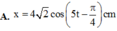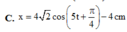Một đĩa nhỏ khối lượng không đáng kể gắn ở đầu một lò xo đặt thẳng đứng trên sàn nằm ngang, độ cứng k=10N/m. Vật có khối lượng m=1kg rơi xuống đĩa từ độ cao 50cm so với đĩa. Giả sử va chạm giữa đĩa và vật là va chạm mềm. Bỏ qua mọi ma sát. Thời gian lò xo bị giãn trong 1 chu kì là:
A 1/3s B 1/4s C 1/2s D 1s
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HY
23 tháng 3 2015
Một vật rơi từ độ cao h xuống đĩa thì vận tốc lúc chạm đĩa tại O của vật cũng chính là vận tốc lớn nhất của con lắc dao động thỏa mãn:
\(v_{max}^2 - v_0^2 = 2gh\)
=> \(v_{max} = \sqrt{2gh} = \sqrt{2.10.1} = \sqrt{20} (m/s)\)
Mà: \(v_{max} = A \omega=> A = \frac{v_{max}}{\omega} = \frac{\sqrt{20}}{10} \approx0,447m.\)
Lực kéo lớn nhất tác dụng lên điểm I chính là lực đàn hồi lớn nhất khi lò xo dãn.nhiều nhất.(ở vị trí biên A)
\(F_ {maxI} = kA = 10.0,447 = 4,47N.\)
Chọn đáp án.B.
VT
20 tháng 11 2019
Chọn D
+ Vận tốc của vật lúc chạm đĩa: 
+ Tần số góc dao động của con lắc lò xo: 
+ Vị trí cân bằng của hệ cách vị trí ban đầu: 
+ Biên độ dao động của hệ: 
+ Năng lượng dao động của vật:
HD
Hà Đức Thọ
Admin
17 tháng 7 2015
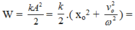
+ Giai đoạn 1: Vật rơi xuống đĩa, vận tốc của vật khi chạm đĩa: \(v=\sqrt{2gh}=\sqrt{2.10.0,5}=\sqrt{10}\)(m/s) = \(100\sqrt{10}\)(cm/s)
Với h = 50 cm là độ cao so với mặt đĩa
+ Giai đoạn 2: Vật và đĩa cùng dao động, là dao động điều hòa.
Ở VTCB, lò xo nén: \(\Delta l_0=\frac{mg}{k}=\frac{0,1.10}{80}=0,0125m=1,25cm\)
Điều đó có nghĩa, sau khi vật chạm mặt đĩa thì nó đang có li độ -1,25cm và vận tốc \(100\sqrt{10}\)(cm/s)
\(\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{80}{0,1}}=20\sqrt{2}\)(rad/s)
Biên độ dao động: \(A=\sqrt{x^2+\frac{v^2}{\omega^2}}=\sqrt{1,25^2+\left(\frac{100\sqrt{10}}{20\sqrt{2}}\right)^2}=11,25cm\)
Lực nén của lò xo lên sàn đạt cực đại khi vật ở vị trí thấp nhất (biên độ dương)
Khi đó, lò xo nén: 11,25 + 1,25 = 12,5cm = 0,125m.
Lực đàn hồi max: \(F_{đh}=80.0,125=10N\)
VT
5 tháng 8 2017
Chọn C
+ Khi chỉ có đĩa M thì độ nén lò xo: 
+ Khi cho thêm vật m thì 
+ Khi xảy ra va chạm thì hệ vật có li độ x = l2 – l1 = 0,1m.
+ Vì vật m rơi tự do nên vận tốc của vật m ngay trước va chạm là: v2 = 2gh =>v = 2m/s.
+ Áp dụng bảo toàn động lượng là: mv = vo(M + m) => vo = 0,5m.
+ Dựa vào chuyển động tròn đều, lúc trước va chạm hệ vật ở vị trí là lúc lò xo nén 10cm hay x0 = - A/√2, vật đi theo chiều dương
VT
10 tháng 4 2018
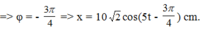
Đáp án C
Vận tốc của vật m ngay khi va chạm vào đĩa M:
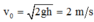
Vận tốc của hệ hai vật sau khi va chạm
= 0,2m/s
Sau khi va chạm hệ hai vật sẽ dao động điều hòa quanh vị trí cân bằng mới, vị trí này cách vị trí cân bằng cũ một đoạn
→ Biên độ dao động của vật là
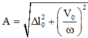
= 4 2 cm
→ Phương trình dao động của vật sẽ là
x = 4 2 cos 5 t + π 4 - 4 cm
VT
4 tháng 8 2019
Đáp án C
+ Vận tốc của m 1 ngay trước khi va chạm vào đĩa cân
→ Vận tốc của hệ hai vật sau va chạm được xác định dựa vào định luật bảo toàn động lượng
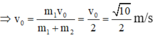
+ Sau va chạm, hệ hai vật sẽ dao động quanh vị trí cân bằng chung của hai vật, vị trí này nằm dưới vị trí cân bằng cũ của đĩa cân một đoạn
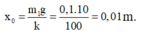
+ Tần số góc của dao động
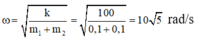
=0,071m =7,1 cm
VT
8 tháng 12 2017
Đáp án C.
– Để vật m không rời khỏi đĩa M thì áp lực của m lên đĩa phải lớn hơn hoặc bằng lực quán tính cực đại tác dụng lên m:
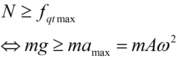
