Cho hình thang vuông ABCD vuông tại A và D. Có hai đáy AB song song với CD. Gọi M là trung điểm của đoạn thẳng AD. Điểm P và Q thuộc BC sao cho BP= CQ . Cho biết rằng MQ vuông góc với DP. Chứng minh rằng MP vuông góc với AQ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 9 2019
Gọi H là trung điểm DC.
Chứng minh HE// IF( vì cùng //BC)
=> HE vuông FK ( vì FK vuông IF)
Tương tự HF// EI( vì cùng //AD)
=> HF vuông EK( vì EK vuông IE)
Xét tam giác EFH có EK và FK là 2 đường cao nên K là trực tâm. Suy ra HK vuông FE mà FE //DC nên HK vuông DC tại H suy ra tam giác KDC cân tại K. Nên KD=KC
31 tháng 8 2019
a) Ta có:
+) M là trung điểm của AD và MN // CD
MN là đường trung bình của hình thang ABCD
N là trung điểm của BC
+) M là trung điểm của AB và ME // AB
ME là đường trung...
7 tháng 7 2018
Gọi N là trung điểm của CD.
Xét \(\Delta\)ABD: M là trung điểm AB; MH // AD; H thuộc BD => H là trung điểm BD
Ta có: OH vuông góc với MH tại H. Mà MH // AD nên OH vuông góc AD
Xét \(\Delta\)ABC: M là trung điểm AB; MK // BC; K thuộc AC => K là trung điểm AC
Lại có: OK vuông góc MK tại K; MK // BC => OK vuông góc BC
Xét \(\Delta\)BDC: H là trung điểm BD; N là trung điểm CD => HN là đường trung bình \(\Delta\)BDC
=> HN // BC. Mà OK vuông góc BC (cmt) => OK vuông góc HN.
Xét \(\Delta\)ADC: K là trung điểm AC; N là trung điểm CD => KN là đường trung bình \(\Delta\)ADC
=> KN // AD. Mà OH vuông góc AD (cmt) => OH vuôn góc KN
Xét \(\Delta\)HNK: OK vuông góc HN; OH vuông góc KN (cmt) => O là trực tâm của \(\Delta\)HNK
=> NO vuông góc KH. Mà HK // DC (Dễ chứng minh) => NO vuông góc DC
Xét \(\Delta\)DOC: ON vuông góc DC (cmt); N là trung điểm DC => \(\Delta\)DOC cân tại O
=> OD = OC => O cách đều 2 điểm C và D (đpcm).
Hình vẽ minh họa, sử dụng tính chất trực tâm của tam giác.
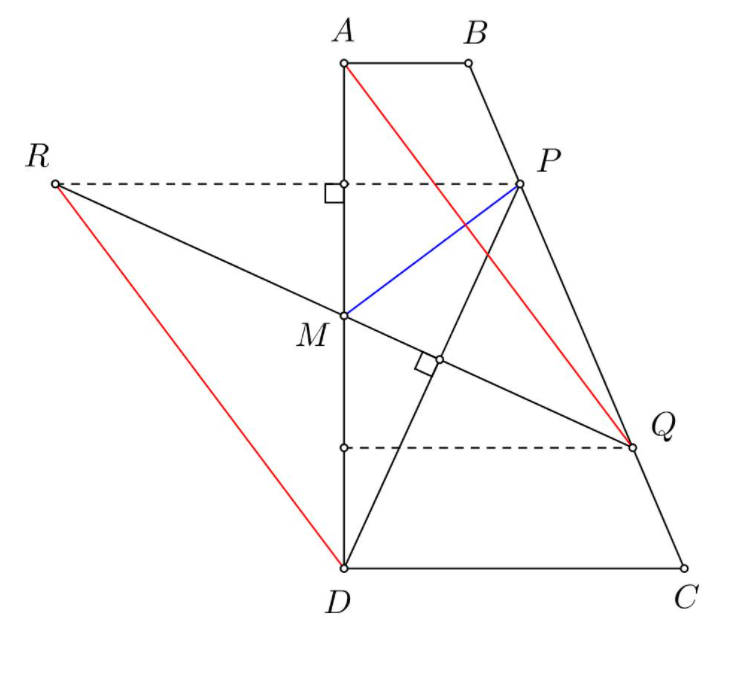
Chứng minh cho M là trực tâm của tam giác RPD