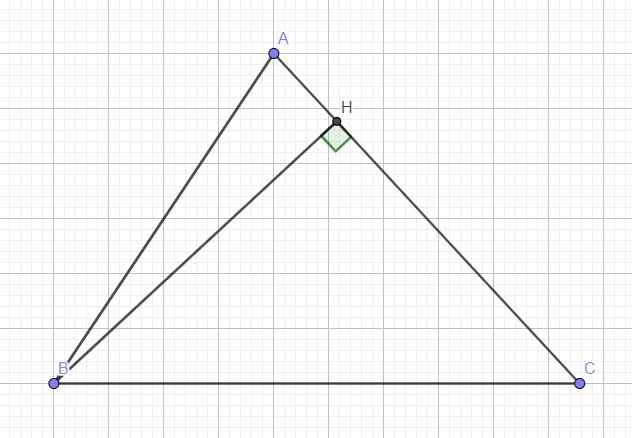
Cho tam giác ABC nhọn(AB<AC) có hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh:Tam giác ABD đồng dạng với tam giác ACE
b) Chứng minh: HD.HB=HE.HC
c) AH cắt BC tại G.Kẻ FI vuông góc với AC tại I.Chứng minh:IF/IC = FA/FC
d) Trên tia đối tia AF lấy điểm N sao cho AN=AF.Gọi M là trung điểm cạnh IC.Chứng minh: NI vuông góc với FM

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc CAE chung
Do đó: ΔABD\(\sim\)ΔACE
b: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)
Do đó: ΔHEB đồng dạng với ΔHDC
SUy ra: HE/HD=HB/HC
hay \(HE\cdot HC=HD\cdot HB\)