mọi người làm giúp em câu c với ạ
em đang cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 10 2023
Câu 7:
a, \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
\(CuO+H_2SO_4\rightarrow CuSO_4+H_2O\)
b, \(n_{H_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
Theo PT: \(n_{Fe}=n_{H_2}=0,1\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Fe}=\dfrac{0,1.56}{10}.100\%=56\%\\\%m_{CuO}=44\%\end{matrix}\right.\)
c, \(n_{CuO}=\dfrac{10-0,1.56}{80}=0,055\left(mol\right)\)
Theo PT: \(n_{H_2SO_4}=n_{Fe}+n_{CuO}=0,155\left(mol\right)\)
\(\Rightarrow C\%_{H_2SO_4}=\dfrac{0,155.98}{100}.100\%=15,19\%\)
d, Theo PT: \(\left\{{}\begin{matrix}n_{FeSO_4}=n_{Fe}=0,1\left(mol\right)\\n_{CuSO_4}=n_{CuO}=0,055\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m_{FeSO_4}=0,1.152=15,2\left(g\right)\\m_{CuSO_4}=0,055.160=8,8\left(g\right)\end{matrix}\right.\)
25 tháng 10 2023
Câu 8:
a, \(CuCO_3+2HCl\rightarrow CuCl_2+CO_2+H_2O\)
b, \(n_{CO_2}=\dfrac{3,36}{22,4}=0,15\left(mol\right)\)
Theo PT: \(n_{CuCO_3}=n_{CO_2}=0,15\left(mol\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{CuCO_3}=\dfrac{0,15.124}{20}.100\%=93\%\\\%m_{CuCl_2}=7\%\end{matrix}\right.\)
c, \(n_{HCl}=2n_{CO_2}=0,3\left(mol\right)\)
\(\Rightarrow C_{M_{HCl}}=\dfrac{0,3}{0,2}=1,5\left(M\right)\)
21 tháng 11 2021
Câu 2.
\(C=\dfrac{N}{20}=\dfrac{4080}{20}=204\)(chu kì)
\(L=\dfrac{N}{2}\cdot3,4=\dfrac{4080}{2}\cdot3,4=6936A^o\)
\(G=X=30\%\cdot4080=1224nu\)
\(A=T=\dfrac{4080-2\cdot1224}{2}=816nu\)
D
1
2 tháng 7 2023
3:
a:Các tia trên hình là Ax,Ay,Bx,By,Cx,Cy
=>Có 6 tia
b: AB<AC
=>B nằm giữa A và C
=>AB+BC=AC
=>BC=4cm
c: AI=3/2=1,5cm
CI=7-1,5=5,5cm
PH
1
26 tháng 11 2023
Câu 1:
\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)
y<=2x+2
=>y-2x-2<=0
Vẽ đường thẳng y=2x+2
Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)
=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y<=-x+5
=>x+y-5<=0
Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)
=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y>=1/2x+2
=>\(-\dfrac{1}{2}x+y-2>=0\)
Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)
=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)
=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)
Vẽ đồ thị:
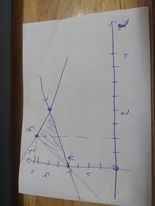
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)
Khi x=0 và y=2 thì F=2-0=2
Khi x=1 và y=4 thì F=4-1=3
Khi x=2 và y=3 thì F=3-2=1
=>Chọn A
ND
1
PN
1
16 tháng 1 2022
Câu 3:
\(\text{Δ}=\left[-2\left(m-1\right)\right]^2-4\left(m^2-3m+4\right)\)
\(=\left(2m-2\right)^2-4\left(m^2-3m+4\right)\)
\(=4m^2-16m+4-4m^2+12m-16=-4m-12\)
Để phương trình có hai nghiệm phân biệt thì -4m-12>0
=>-4m>12
hay m<-3
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3m+4\end{matrix}\right.\)
Theo đề, ta có: \(x_1+x_2=x_1x_2\)
\(\Leftrightarrow m^2-3m+4-2m+2=0\)
=>(m-2)(m-3)=0
hay \(m\in\varnothing\)
S
1
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2021
Do vai trò của 3 biến là như nhau, không mất tính tổng quát giả sử \(x>y>z\)
Ta có: \(x-z=\left(x-y\right)+\left(y-z\right)\)
Đặt \(\left\{{}\begin{matrix}x-y=a>0\\y-z=b>0\end{matrix}\right.\)
Do \(x;z\in\left[0;2\right]\Rightarrow x-z\le2\) hay \(a+b\le2\)
Ta có:
\(P=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\ge\dfrac{1}{2}\left(\dfrac{4}{a+b}\right)^2+\dfrac{1}{\left(a+b\right)^2}\)
\(P\ge\dfrac{9}{\left(a+b\right)^2}\ge\dfrac{9}{2^2}=\dfrac{9}{4}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=b\\a+b=2\\\end{matrix}\right.\) \(\Rightarrow a=b=1\) hay \(\left(x;y;z\right)=\left(0;1;2\right)\) và các hoán vị
LM
1
OD
0
MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)