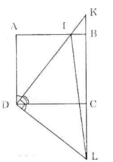
Cho hình vuông ABCD. Gọi I là một điểm nẳm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng :
a) Tam giác DIL là một tam giác cân
b) Tổng \(\dfrac{1}{DI^2}+\dfrac{1}{DK^2}\) không đổi khi I thay đổi trên cạnh AB

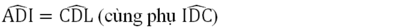
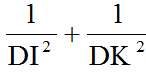
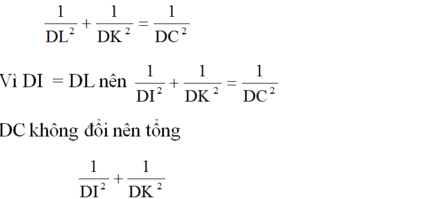
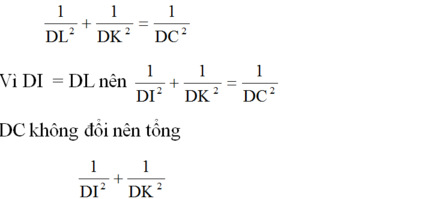

a) ΔADI và ΔCDL có: góc A = góc C = 90°
AD = CD (hai cạnh hình vuông)
góc D1 = góc D2
cùng phụ với góc CDI
Do đó ΔADI = ΔCDL (g.c.g)
Suy ra DI = DL. Vậy ΔDIL cân
b) Áp dụng hệ thức là không đổi.
là không đổi.
Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều phải chứng minh ở câu b) rất gần với hệ thức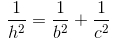
Nếu đề bài không cho vẽ DL ⊥ DK thì ta vẫn phải vẽ đường phụ DL ⊥ DK để có thể vận dụng hệ thức trên.
Lời giải: