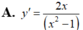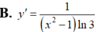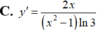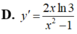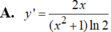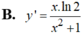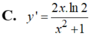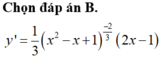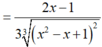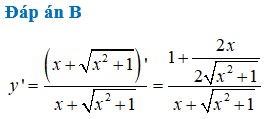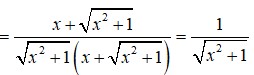tính đạo hàm của: tan3(x2+1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 5 2021
\(y'=3tan^2x.\left[tan\left(2x\right)\right]'+3cot^2x.\left[cot\left(2x\right)\right]'\)
\(=3tan^2x.2.\dfrac{1}{cos^22x}-3cot^2x.2.\dfrac{1}{sin^22x}\)
\(=\dfrac{6tan^2x}{cos^22x}-\dfrac{6cot^2x}{sin^22x}\)
CM
20 tháng 9 2019
Chọn C.
Đầu tiên sử dụng quy tắc nhân.
y' = [(x2 – x + 1)3]’(x2 + x + 1)2 + [(x2 + x + 1)2]’(x2 – x + 1)3.
Sau đó sử dụng công thức 
y' = 3(x2 – x + 1)2(x2 – x + 1)’(x2 + x + 1) + 2(x2 + x + 1)(x2 + x + 1)’(x2 – x + 1)3
y’ = 3(x2 – x + 1)2(2x – 1)(x2 + x + 1)2 + 2(x2 + x + 1)(2x + 1)(x2 – x + 1)3
y’ = (x2 – x + 1)2(x2 + x + 1)[3(2x – 1)(x2 + x + 1) + 2(2x + 1)(x2 – x + 1)].
CM
25 tháng 1 2018
Chọn B.
Sử dụng công thức u / với u = 1 + 2 x − x 2
y ' = 1 + 2 x − x 2 / 1 + 2 x − x 2 = 1 − x 1 + 2 x − x 2
PT
1
