rút gọn biểu thức

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,ĐK:x\ne\pm1;x\ne0\\ M=\dfrac{1-x+2x}{\left(1+x\right)\left(1-x\right)}:\dfrac{1-x}{x}\\ M=\dfrac{x+1}{\left(x+1\right)\left(1-x\right)}\cdot\dfrac{x}{1-x}=\dfrac{x}{\left(1-x\right)^2}\\ b,ĐK:x\ge0;x\ne4\\ N=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ N=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
Tất cả đều phải tìm điều kiện

\(\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}=\dfrac{\left(x-2\right)^2}{x^3-2x^2-4x+8}\)
Để biểu thức trên nhận giá trị âm khi \(\dfrac{\left(x-2\right)^2}{x^3-2x^2-4x+8}< 0\)
\(\Rightarrow x^3-2x^2-4x+8< 0\)do \(\left(x-2\right)^2\ge0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+4\right)-2x\left(x+2\right)< 0\)
\(\Leftrightarrow\left(x+2\right)\left(x-2\right)^2< 0\Leftrightarrow x< -2\)

\(\dfrac{8-2x}{x^2+x-20}=-\dfrac{2\left(4-x\right)}{\left(4-x\right)\left(x+5\right)}=\dfrac{-2}{x+5}\)
Để biểu thức trên nhận giá trị dương khi
\(x+5< 0\)do -2 < 0
\(\Leftrightarrow x< -5\)

Thay 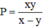 vào biểu thức ta được:
vào biểu thức ta được:
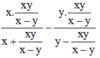
Ta có:
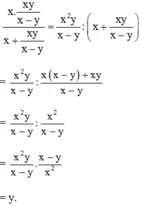
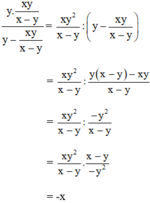
Vậy giá trị biểu thức bằng y – (-x) = x + y.

a) a ≠ 0 , a ≠ − 5
b) Ta có A = a 3 + 4 a 2 − 5 a 2 a ( a + 5 ) = a ( a − 1 ) ( a + 5 ) 2 a ( a + 5 ) = a − 1 2
c) Thay a = -1 (TMĐK) vào a ta được A = -1
d) Ta có A = 0 Û a = 1 (TMĐK)

a) Thay phân thức P vào biểu thức A rồi rút gọn chúng ta thu được A = u + v với điều kiện các biểu thức có nghĩa.
b) Tương tự a) ta có B = 1.
\(\left(\dfrac{x\sqrt{x}+1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}+\dfrac{x+1}{\sqrt{x}}\right)\) điều kiện xát định :(x > 0 ; x \(\ne\) 1 )
= \(\left(\dfrac{x\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{x\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x+1}{\sqrt{x}}\right)\)
= \(\dfrac{\left(x\sqrt{x}+1\right)\left(\sqrt{x}+1\right)-\left(x\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(x-1\right)}+\dfrac{x+1}{\sqrt{x}}\)
= \(\dfrac{x^2+x\sqrt{x}+\sqrt{x}+1-\left(x^2-x\sqrt{x}+\sqrt{x}-1\right)}{\sqrt{x}\left(x-1\right)}+\dfrac{x+1}{\sqrt{x}}\)
= \(\dfrac{x^2+x\sqrt{x}+\sqrt{x}+1-x^2+x\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(x-1\right)}+\dfrac{x+1}{\sqrt{x}}\)
= \(\dfrac{2x\sqrt{x}+2}{\sqrt{x}\left(x-1\right)}+\dfrac{x+1}{\sqrt{x}}\) = \(\dfrac{2x\sqrt{x}+2+\left(\left(x+1\right)\left(x-1\right)\right)}{\sqrt{x}\left(x-1\right)}\)
= \(\dfrac{2x\sqrt{x}+2+x^2-1}{\sqrt{x}\left(x-1\right)}\) = \(\dfrac{2x\sqrt{x}+x^2+1}{\sqrt{x}\left(x-1\right)}\)