Một ấm điện có ghi 220V - 1 000W được sử dụng với hiệu điện thế 220V để đun sôi 2l nước từ nhiệt độ ban đầu là 20oC. Bỏ qua nhiệt lượng làm nóng vỏ ấm và nhiệt lượng tỏa vào môi trường, tính thời gian đun sôi nước. Biết nhiệt dung riêng của nước 4 200J/kg.K.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
3 tháng 10 2018
Vì hiệu điện thế định mức của ấm bằng hiệu điện thế được sử dụng nên ấm hoạt động bình thường
V
21 tháng 12 2022
a, Đổi: 1 lít nước = 1 kg nước
Nhiệt lượng cần thiết để đun sôi ấm nước:
Qich = m.c.Δt = 2.4200.(100-20) = 672000(J)
Vì bỏ qua nhiệt lượng làm nóng vỏ ấm và nhiệt lượng thoát ra môi trường nên: Qich = Qtp:
Qtp = P.t ⇒ t = \(\dfrac{Qtp}{P}=\dfrac{672000}{1000}=672\left(s\right)=11,2\)(phút)
b,Đổi: 30 phút = 0,5 giờ; 1000W = 1kW
Số tiền phải trả: 1500. (1 . 0,5 . 30) = 22500 (đồng)
19 tháng 12 2022
a)Điện trở ấm: \(R_{ấm}=\dfrac{U^2}{P}=\dfrac{220^2}{1000}=48,4\Omega\)
Nhiệt lượng cần thiết để đun sôi nước:
\(Q=mc\left(t_2-t_1\right)=2\cdot4200\cdot\left(100-20\right)=672000J\)
Mặt khác: \(Q=RI^2t=\dfrac{U^2}{R}\cdot t\)
\(\Rightarrow t=\dfrac{Q\cdot R}{U^2}=\dfrac{672000\cdot48,4}{220^2}=672s=1h52phút\)
b)Dòng điện qua ấm:
\(I=\dfrac{U}{R}=\dfrac{220}{48,4}=\dfrac{50}{11}A\)
27 tháng 11 2021
Nhiệt lượng cung cấp để đun sôi nước:
\(A=Q=mc\Delta t=5\cdot4200\cdot\left(100-20\right)=1680000J\)
Thời gian đun sôi nước:
\(t=\dfrac{A}{UI}=\dfrac{1680000}{220\cdot\dfrac{1000}{220}}=1680s\)
Chọn D
VT
7 tháng 7 2019
Thể tích nước: V = 1,5 lít Þ m = 1,5 kg.
Nhiệt lượng cần thiết để ấm nước sôi là: Qi = m.c.Dt = 1,5.4200.(100 – 24) = 478800 J.
Bỏ qua sự nhiệt lượng làm nóng vỏ ấm và nhiệt lượng tỏa ra môi trường ngoài nên coi rằng hiệu suất là H = 100%.
Þ Nhiệt lượng mà bếp cung cấp là: Qtp = 478800 J.
Ấm điện có ghi 220V - 700W được sử dụng với hiệu điện thế đúng 220V nên công suất của bếp khi đun là P = 700W.
Thời gian đun t = Qtp/P = 478800/700 = 684 giây. Chọn đáp án B.
N
20 tháng 11 2021
Bỏ qua nhiệt độ làm ấm vỏ điện và nhiệt lượng tỏa ra môi trường ngoài.
\(\Rightarrow Q_{toa}=Q_{thu}=mc\Delta t=2\cdot4200\cdot80=672000\left(J\right)\)
Ta có: \(Q_{toa}=A=Pt\Rightarrow t=\dfrac{Q_{toa}}{P}=\dfrac{672000}{1000}=672\left(s\right)\)
Vậy....................
20 tháng 11 2021
Nhiệt lượng bếp tỏa:
\(Q=mc\Delta t=2\cdot4200\cdot\left(100-20\right)=672000J\)
Điện trở ấm:
\(R=\dfrac{U^2}{P}=\dfrac{220^2}{1000}=48,4\Omega\)
Dòng điện qua ấm:
\(I=\dfrac{U}{R}=\dfrac{220}{48,4}=\dfrac{50}{11}A\)
Thời gian cần để đun ấm:
\(t=\dfrac{A}{R\cdot I^2}=\dfrac{Q}{R\cdot I^2}=\dfrac{672000}{48,4\cdot\left(\dfrac{50}{11}\right)^2}=672s\)
Ấm điện được dùng hiệu điện thế đúng bằng hiệu điện thế định mức nên công suất P của nó cũng chính bằng công suất định mức (1000W).
Bỏ qua nhiệt lượng làm nóng vỏ ấm và nhiệt lượng tỏa vào môi trường, nên nhiệt lượng Q để đun sôi nước sẽ chính bằng lượng điện năng A mà ấm đã tiêu thụ. Ta có A = Q, tức là Pt = cm(t2 – t1), từ đó suy ra
t =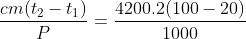
= 672 s.
Ấm điện được dùng hiệu điện thế đúng bằng hiệu điện thế định mức nên công suất P của nó cũng chính bằng công suất định mức (1000W).
Bỏ qua nhiệt lượng làm nóng vỏ ấm và nhiệt lượng tỏa vào môi trường, nên nhiệt lượng Q để đun sôi nước sẽ chính bằng lượng điện năng A mà ấm đã tiêu thụ.
Ta có:
+ A=PtA=Pt
+ Q=mcΔtQ=mcΔt
Lại có:
A=QA=Q, tức là Pt=cm(t2–t1)Pt=cm(t2–t1), từ đó suy ra:
t=cm(t2−t1)P=4200.2(100−20)1000=672st=cm(t2−t1)P=4200.2(100−20)1000=672s.